John R. Stallings
Encyclopedia
John Robert Stallings Jr. (July 22, 1935 – November 24, 2008) was a mathematician
known for his seminal contributions to geometric group theory
and 3-manifold topology
. Stallings was a Professor Emeritus in the Department of Mathematics at the University of California at Berkeley where he had been a faculty member since 1967. He published over 50 papers, predominantly in the areas of geometric group theory
and the topology of 3-manifold
s. Stallings' most important contributions include a proof, in a 1960 paper, of the Poincaré Conjecture in dimensions greater than six
and a proof, in a 1971 paper, of the Stallings theorem about ends of groups
.
.
Stallings received his B.Sc. from University of Arkansas
in 1956 (where he was one of the first two graduates in the university's Honors program) and he received a Ph.D. in Mathematics from Princeton University
in 1959 under the direction of Ralph Fox
.
After completing his PhD, Stallings held a number of postdoctoral and faculty positions, including being an NSF postdoctoral fellow at Oxford University as well as and instructorship and a faculty appointment at Princeton. Stallings joined the University of California at Berkeley as a faculty member in 1967 where he remained until his retirement in 1994. Even after his retirement, Stallings continued supervising UC Berkeley graduate students until 2005. Stallings was an Alfred P. Sloan Research fellow
from 1962–65 and a Miller Institute fellow from 1972-73.
Over the course of his career, Stallings had 22 doctoral students and 60 doctoral descendants. He published over 50 papers, predominantly in the areas of geometric group theory
and the topology of 3-manifold
s.
Stallings delivered an invited address as the International Congress of Mathematicians
in Nice
in 1970 and a James K. Whittemore Lecture at Yale University
in 1969.
Stallings received the Frank Nelson Cole Prize in Algebra
from the American Mathematical Society
in 1970.
The conference "Geometric and Topological Aspects of Group Theory", held at the Mathematical Sciences Research Institute
in Berkeley in May 2000, was dedicated to the 65th birthday of Stallings.
In 2002 a special issue of the journal Geometriae Dedicata
was dedicated to Stallings on the occasion of his 65th birthday. Stallings died from prostate cancer
on November 24, 2008.
and low-dimensional topology
(particularly the topology of 3-manifold
s) and on the interplay between these two areas.
An early significant result of Stallings is his 1960 proof of the Poincaré Conjecture in dimensions greater than six
. (Stallings' proof was obtained independently from and shortly after the different proof of Steve Smale who established the same result in dimensions bigger than four).
Using "engulfing" methods similar to those in his proof of the Poincaré Conjecture for n > 6, Stallings proved that ordinary Euclidean n-dimensional space has a unique piecewise linear, hence also smooth, structure, if n is not equal to 4. This took on added significance when, as a consequence of work of Michael Freedman
and Simon Donaldson
in 1982, it was shown that 4-space has exotic smooth structures
, in fact uncountably many such.
In a 1963 paper Stallings constructed an example of a finitely presented group with infinitely generated 3-dimensional integral homology group and, moreover, not of the type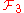
, that is, not admitting a classifying space
with a finite 3-skeleton. This example came to be called the Stallings group and is a key example in the study of homological finiteness properties of groups. Bieri later showed that the Stallings group is exactly the kernel of the homomorphism from the direct product of three copies of the free group
F2 to the additive group Z of integers that sends to 1 ∈ Z the six elements coming from the choice of free bases for the three copies of F2. Bieri also showed that the Stallings group fits into a sequence of examples of groups of type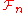
but not of type 
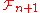. The Stallings group is a key object in the version of discrete Morse theory
for cubical complexes developed by Bestvina
and Brady and in the study of subgroups of direct products of limit groups.
Stallings' most famous theorem in group theory
is an algebraic characterization of groups with more than one end (that is, with more than one "connected component at infinity"), which is now known as Stallings' theorem about ends of groups
. Stallings proved that a finitely generated group G has more than one end if and only if this group admits a nontrivial splitting as an amalgamated free product or as an HNN-extension over a finite group (that is, in terms of Bass-Serre theory, if and only if the group admits a nontrivial action on a tree
with finite edge stabilizers). More precisely, the theorem states that a finitely generated group G has more than one end if and only if either G admits a splitting as an amalgamated free product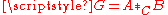
, where the group C is finite and C ≠ A, C ≠ B, or G admits a splitting as an HNN-extension 
where K,L ≤ H are finite subgroup
s of H.
Stallings proved this result in a series of works, first dealing with the torsion-free case (that is, a group with no nontrivial elements of finite order
) and then with the general case. Stalling's theorem yielded a positive solution to the long-standing open problem about characterizing finitely generated groups of cohomological dimension one as exactly the free group
s. Stallings' theorem about ends of groups is considered one of the first results in geometric group theory
proper since it connects a geometric property of a group (having more than one end) with its algebraic structure (admitting a splitting over a finite subgroup). Stallings' theorem spawned many subsequent alternative proofs by other mathematicians (e.g.) as well as many applications (e.g.). The theorem also motivated several generalizations and relative versions of Stallings' result to other contexts, such as the study of the notion of relative ends of a group with respect to a subgroup, including a connection to CAT(0) cubical complexes. A comprehensive survey discussing, in particular, numerous applications and generalizations of Stallings' theorem, is given in a 2003 paper of Wall.
Another influential paper of Stalling is his 1983 article "Topology on finite graphs". Traditionally, the algebraic structure of subgroup
s of free group
s has been studied in combinatorial group theory
using combinatorial methods, such as the Schreier rewriting method
and Nielsen transformation
s. Stallings' paper put forward a topological approach based on the methods of covering space theory that also used a simple graph-theoretic
framework. The paper introduced the notion of what is now commonly referred to as Stallings subgroup graph for describing subgroups of free groups, and also introduced a foldings technique (used for approximating and algorithmically obtaining the subgroup graphs) and the notion of what is now known as a Stallings folding. Most classical results regarding subgroups of free groups acquired simple and straightforward proofs in this set-up and Stallings' method has become the standard tool in the theory for studying the subgroup structure of free groups, including both the algebraic and algorithmic questions (see ). In particular, Stallings subgroup graphs and Stallings foldings have been the used as a key tools in many attempts to approach the Hanna Neumann conjecture
.
Stallings subgroup graphs can also be viewed as finite state automata and they have also found applications in semigroup theory
and in computer science
.
Stallings' foldings method has been generalized and applied to other contexts, particularly in Bass-Serre theory for approximating group actions on trees
and studying the subgroup structure of the fundamental groups of graphs of groups. The first paper in this direction was written by Stallings himself, with several subsequent generalizations of Stallings' folding methods in the Bass-Serre theory context by other mathematicians.
Stallings' 1991 paper "Non-positively curved triangles of groups" introduced and studied the notion of a triangle of groups. This notion was the starting point for the theory of complexes of groups (a higher-dimensional analog of Bass-Serre theory), developed by Haefliger and others. Stallings' work pointed out the importance of imposing some sort of "non-positive curvature" conditions on the complexes of groups in order for the theory to work well; such restrictions are not necessary in the one-dimensional case of Bass-Serre theory.
Among Stallings' contributions to 3-manifold topology
, the most well-known is the Stallings fibration theorem. The theorem states that if M is a compact irreducible 3-manifold
whose fundamental group
contains a normal subgroup
, such that this subgroup is finitely generated and such that the quotient group
by this subgroup is infinite cyclic, then M fibers
over a circle. This is an important structural result in the theory of Haken manifold
s that engendered many alternative proofs, generalizations and applications (e.g. ), including a higher-dimensional analog.
A 1965 paper of Stallings "How not to prove the Poincaré conjecture" gave a group-theoretic
reformulation of the famous Poincaré conjecture
. The paper began with a humorous admission: "I have committed the sin of falsely proving Poincare's Conjecture. But that was in another country; and besides, until now, no one has known about it." Despite its ironic title, Stallings' paper informed much of the subsequent research on exploring the algebraic aspects of the Poincaré Conjecture
(see, for example,).
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
known for his seminal contributions to geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
and 3-manifold topology
Low-dimensional topology
In mathematics, low-dimensional topology is the branch of topology that studies manifolds of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology.A number of...
. Stallings was a Professor Emeritus in the Department of Mathematics at the University of California at Berkeley where he had been a faculty member since 1967. He published over 50 papers, predominantly in the areas of geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
and the topology of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s. Stallings' most important contributions include a proof, in a 1960 paper, of the Poincaré Conjecture in dimensions greater than six
Generalized Poincaré conjecture
In the mathematical area of topology, the term Generalized Poincaré conjecture refers to a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a...
and a proof, in a 1971 paper, of the Stallings theorem about ends of groups
Stallings theorem about ends of groups
In the mathematical subject of group theory, the Stallings theorem about ends of groups states that a finitely generated group G has more than one end if and only if the group G admits a nontrivial decomposition as an amalgamated free product or an HNN extension over a finite subgroup...
.
Biographical data
John Stallings was born on July 22, 1935 in Morrilton, ArkansasMorrilton, Arkansas
Morrilton is a city in Conway County, Arkansas, United States, northwest of Little Rock. The town was home to Harding College, now Harding University of Searcy, Arkansas, for about a decade in the 1920s and 1930s. The population was 6,550 at the 2000 census...
.
Stallings received his B.Sc. from University of Arkansas
University of Arkansas
The University of Arkansas is a public, co-educational, land-grant, space-grant, research university. It is classified by the Carnegie Foundation as a research university with very high research activity. It is the flagship campus of the University of Arkansas System and is located in...
in 1956 (where he was one of the first two graduates in the university's Honors program) and he received a Ph.D. in Mathematics from Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
in 1959 under the direction of Ralph Fox
Ralph Fox
Ralph Hartzler Fox was an American mathematician. As a professor at Princeton University, he taught and advised many of the contributors to the Golden Age of differential topology, and he played an important role in the modernization and main-streaming of knot theory.Ralph Fox attended Swarthmore...
.
After completing his PhD, Stallings held a number of postdoctoral and faculty positions, including being an NSF postdoctoral fellow at Oxford University as well as and instructorship and a faculty appointment at Princeton. Stallings joined the University of California at Berkeley as a faculty member in 1967 where he remained until his retirement in 1994. Even after his retirement, Stallings continued supervising UC Berkeley graduate students until 2005. Stallings was an Alfred P. Sloan Research fellow
Sloan Fellowship
The Sloan Research Fellowships are awarded annually by the Alfred P. Sloan Foundation since 1955 to "provide support and recognition to early-career scientists and scholars". This is distinct from the Sloan Fellows in business....
from 1962–65 and a Miller Institute fellow from 1972-73.
Over the course of his career, Stallings had 22 doctoral students and 60 doctoral descendants. He published over 50 papers, predominantly in the areas of geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
and the topology of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s.
Stallings delivered an invited address as the International Congress of Mathematicians
International Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
in Nice
Nice
Nice is the fifth most populous city in France, after Paris, Marseille, Lyon and Toulouse, with a population of 348,721 within its administrative limits on a land area of . The urban area of Nice extends beyond the administrative city limits with a population of more than 955,000 on an area of...
in 1970 and a James K. Whittemore Lecture at Yale University
Yale University
Yale University is a private, Ivy League university located in New Haven, Connecticut, United States. Founded in 1701 in the Colony of Connecticut, the university is the third-oldest institution of higher education in the United States...
in 1969.
Stallings received the Frank Nelson Cole Prize in Algebra
Cole Prize
The Frank Nelson Cole Prize, or Cole Prize for short, is one of two prizes awarded to mathematicians by the American Mathematical Society, one for an outstanding contribution to algebra, and the other for an outstanding contribution to number theory. The prize is named after Frank Nelson Cole, who...
from the American Mathematical Society
American Mathematical Society
The American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...
in 1970.
The conference "Geometric and Topological Aspects of Group Theory", held at the Mathematical Sciences Research Institute
Mathematical Sciences Research Institute
The Mathematical Sciences Research Institute , founded in 1982, is an independent nonprofit mathematical research institution whose funding sources include the National Science Foundation, foundations, corporations, and more than 90 universities and institutions...
in Berkeley in May 2000, was dedicated to the 65th birthday of Stallings.
In 2002 a special issue of the journal Geometriae Dedicata
Geometriae Dedicata
Geometriae Dedicata is a mathematical journal, founded in 1972, concentrating on geometry and its relationship to topology, group theory and the theory of dynamical systems. It was created on the initiative of Hans Freudenthal in Utrecht, the Netherlands. It is published by Springer Netherlands....
was dedicated to Stallings on the occasion of his 65th birthday. Stallings died from prostate cancer
Prostate cancer
Prostate cancer is a form of cancer that develops in the prostate, a gland in the male reproductive system. Most prostate cancers are slow growing; however, there are cases of aggressive prostate cancers. The cancer cells may metastasize from the prostate to other parts of the body, particularly...
on November 24, 2008.
Mathematical contributions
Most of Stallings' mathematical contributions are in the areas of geometric group theoryGeometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
and low-dimensional topology
Low-dimensional topology
In mathematics, low-dimensional topology is the branch of topology that studies manifolds of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology.A number of...
(particularly the topology of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s) and on the interplay between these two areas.
An early significant result of Stallings is his 1960 proof of the Poincaré Conjecture in dimensions greater than six
Generalized Poincaré conjecture
In the mathematical area of topology, the term Generalized Poincaré conjecture refers to a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a...
. (Stallings' proof was obtained independently from and shortly after the different proof of Steve Smale who established the same result in dimensions bigger than four).
Using "engulfing" methods similar to those in his proof of the Poincaré Conjecture for n > 6, Stallings proved that ordinary Euclidean n-dimensional space has a unique piecewise linear, hence also smooth, structure, if n is not equal to 4. This took on added significance when, as a consequence of work of Michael Freedman
Michael Freedman
Michael Hartley Freedman is a mathematician at Microsoft Station Q, a research group at the University of California, Santa Barbara. In 1986, he was awarded a Fields Medal for his work on the Poincaré conjecture. Freedman and Robion Kirby showed that an exotic R4 manifold exists.Freedman was born...
and Simon Donaldson
Simon Donaldson
Simon Kirwan Donaldson FRS , is an English mathematician known for his work on the topology of smooth four-dimensional manifolds. He is now Royal Society research professor in Pure Mathematics and President of the Institute for Mathematical Science at Imperial College London...
in 1982, it was shown that 4-space has exotic smooth structures
Exotic R4
In mathematics, an exotic R4 is a differentiable manifold that is homeomorphic to the Euclidean space R4, but not diffeomorphic.The first examples were found by Robion Kirby and Michael Freedman, by using the contrast between Freedman's theorems about topological 4-manifolds, and Simon Donaldson's...
, in fact uncountably many such.
In a 1963 paper Stallings constructed an example of a finitely presented group with infinitely generated 3-dimensional integral homology group and, moreover, not of the type
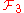, that is, not admitting a classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
with a finite 3-skeleton. This example came to be called the Stallings group and is a key example in the study of homological finiteness properties of groups. Bieri later showed that the Stallings group is exactly the kernel of the homomorphism from the direct product of three copies of the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
F2 to the additive group Z of integers that sends to 1 ∈ Z the six elements coming from the choice of free bases for the three copies of F2. Bieri also showed that the Stallings group fits into a sequence of examples of groups of type
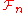but not of type 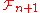. The Stallings group is a key object in the version of discrete Morse theoryMorse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
for cubical complexes developed by Bestvina
Mladen Bestvina
Mladen Bestvina is a Croatian American mathematician working in the area of geometric group theory. He is a Distinguished Professor in the Department of Mathematics at the University of Utah.-Biographical info:...
and Brady and in the study of subgroups of direct products of limit groups.
Stallings' most famous theorem in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
is an algebraic characterization of groups with more than one end (that is, with more than one "connected component at infinity"), which is now known as Stallings' theorem about ends of groups
Stallings theorem about ends of groups
In the mathematical subject of group theory, the Stallings theorem about ends of groups states that a finitely generated group G has more than one end if and only if the group G admits a nontrivial decomposition as an amalgamated free product or an HNN extension over a finite subgroup...
. Stallings proved that a finitely generated group G has more than one end if and only if this group admits a nontrivial splitting as an amalgamated free product or as an HNN-extension over a finite group (that is, in terms of Bass-Serre theory, if and only if the group admits a nontrivial action on a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
with finite edge stabilizers). More precisely, the theorem states that a finitely generated group G has more than one end if and only if either G admits a splitting as an amalgamated free product
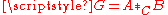, where the group C is finite and C ≠ A, C ≠ B, or G admits a splitting as an HNN-extension where K,L ≤ H are finite subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of H.
Stallings proved this result in a series of works, first dealing with the torsion-free case (that is, a group with no nontrivial elements of finite order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
) and then with the general case. Stalling's theorem yielded a positive solution to the long-standing open problem about characterizing finitely generated groups of cohomological dimension one as exactly the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s. Stallings' theorem about ends of groups is considered one of the first results in geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
proper since it connects a geometric property of a group (having more than one end) with its algebraic structure (admitting a splitting over a finite subgroup). Stallings' theorem spawned many subsequent alternative proofs by other mathematicians (e.g.) as well as many applications (e.g.). The theorem also motivated several generalizations and relative versions of Stallings' result to other contexts, such as the study of the notion of relative ends of a group with respect to a subgroup, including a connection to CAT(0) cubical complexes. A comprehensive survey discussing, in particular, numerous applications and generalizations of Stallings' theorem, is given in a 2003 paper of Wall.
Another influential paper of Stalling is his 1983 article "Topology on finite graphs". Traditionally, the algebraic structure of subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s has been studied in combinatorial group theory
Combinatorial group theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
using combinatorial methods, such as the Schreier rewriting method
Schreier's subgroup lemma
Schreier's subgroup lemma is a theorem in group theory used in the Schreier–Sims algorithm and also for finding a presentation of a subgroup.-Definition:Suppose H is a subgroup of G, which is finitely generated with generating set S, that is, G = ....
and Nielsen transformation
Nielsen transformation
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, Nielsen transformations, named after Jakob Nielsen, are certain automorphisms of a free group which are a non-commutative analogue of row reduction and one of the main tools used in studying free groups,...
s. Stallings' paper put forward a topological approach based on the methods of covering space theory that also used a simple graph-theoretic
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
framework. The paper introduced the notion of what is now commonly referred to as Stallings subgroup graph for describing subgroups of free groups, and also introduced a foldings technique (used for approximating and algorithmically obtaining the subgroup graphs) and the notion of what is now known as a Stallings folding. Most classical results regarding subgroups of free groups acquired simple and straightforward proofs in this set-up and Stallings' method has become the standard tool in the theory for studying the subgroup structure of free groups, including both the algebraic and algorithmic questions (see ). In particular, Stallings subgroup graphs and Stallings foldings have been the used as a key tools in many attempts to approach the Hanna Neumann conjecture
Hanna Neumann conjecture
In the mathematical subject of group theory, the Hanna Neumann conjecture is a statement about the rank of the intersection of two finitely generated subgroups of a free group. The conjecture was posed by Hanna Neumann in 1957...
.
Stallings subgroup graphs can also be viewed as finite state automata and they have also found applications in semigroup theory
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
and in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.
Stallings' foldings method has been generalized and applied to other contexts, particularly in Bass-Serre theory for approximating group actions on trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
and studying the subgroup structure of the fundamental groups of graphs of groups. The first paper in this direction was written by Stallings himself, with several subsequent generalizations of Stallings' folding methods in the Bass-Serre theory context by other mathematicians.
Stallings' 1991 paper "Non-positively curved triangles of groups" introduced and studied the notion of a triangle of groups. This notion was the starting point for the theory of complexes of groups (a higher-dimensional analog of Bass-Serre theory), developed by Haefliger and others. Stallings' work pointed out the importance of imposing some sort of "non-positive curvature" conditions on the complexes of groups in order for the theory to work well; such restrictions are not necessary in the one-dimensional case of Bass-Serre theory.
Among Stallings' contributions to 3-manifold topology
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
, the most well-known is the Stallings fibration theorem. The theorem states that if M is a compact irreducible 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
whose fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
contains a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, such that this subgroup is finitely generated and such that the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
by this subgroup is infinite cyclic, then M fibers
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
over a circle. This is an important structural result in the theory of Haken manifold
Haken manifold
In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...
s that engendered many alternative proofs, generalizations and applications (e.g. ), including a higher-dimensional analog.
A 1965 paper of Stallings "How not to prove the Poincaré conjecture" gave a group-theoretic
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
reformulation of the famous Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
. The paper began with a humorous admission: "I have committed the sin of falsely proving Poincare's Conjecture. But that was in another country; and besides, until now, no one has known about it." Despite its ironic title, Stallings' paper informed much of the subsequent research on exploring the algebraic aspects of the Poincaré Conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
(see, for example,).
External links
- home page of John Stallings.
- Remembering John Stallings, Notices of the American Mathematical SocietyNotices of the American Mathematical SocietyNotices of the American Mathematical Society is a membership magazine of the American Mathematical Society, published monthly except for the combined June/July issue. It is the world's most widely read mathematics magazine, sent to the approximately 30,000 AMS members worldwide...
, vol. 56 (2009), no. 11, pp. 1410 1417