Stallings theorem about ends of groups
Encyclopedia
In the mathematical subject of group theory
, the Stallings theorem about ends of groups states that a finitely generated group G has more than one end if and only if the group G admits a nontrivial decomposition as an amalgamated free product or an HNN extension
over a finite subgroup
. In the modern language of Bass–Serre theory
the theorem says that a finitely generated group G has more than one end if and only if G admits a nontrivial (that is, without a global fixed point) action
on a simplicial tree
with finite edge-stabilizers and without edge-inversions.
The theorem was proved by John R. Stallings
, first in the torsion-free case (1968) and then in the general case (1971).
where the degree of every vertex is finite. One can view Γ as a topological space
by giving it the natural structure of a one-dimensional cell complex. Then the ends of Γ are the ends of this topological space. A more explicit definition of the number of ends of a graph is presented below for completeness.
Let n ≥ 0 be a non-negative integer. The graph Γ is said to satisfy e(Γ) ≤ n if for every finite collection F of edges of Γ the graph Γ − F has at most n infinite connected components. By definition, e(Γ) = m if e(Γ) ≤ m and if for every 0 ≤ n < m the statement e(Γ) ≤ n is false. Thus e(Γ) = m if m is the smallest nonnegative integer n such that e(Γ) ≤ n. If there does not exist an integer n ≥ 0 such that e(Γ) ≤ n, put e(Γ) = ∞. The number e(Γ) is called the number of ends of Γ.
Informally, e(Γ) is the number of "connected components at infinity" of Γ. If e(Γ) = m < ∞, then for any finite set F of edges of Γ there exists a finite set K of edges of Γ with F ⊆ K such that Γ − F has exactly m infinite connected component
s. If e(Γ) = ∞, then for any finite set F of edges of Γ and for any integer n ≥ 0 there exists a finite set K of edges of Γ with F ⊆ K such that Γ − K has at least n infinite connected components.
of G and let Γ(G, S) be the Cayley graph
of G with respect to S. The number of ends of G is defined as e(G) = e(Γ(G, S)). A basic fact in the theory of ends of groups says that e(Γ(G, S)) does not depend on the choice of a finite generating set
S of G, so that e(G) is well-defined.
of G and let Γ = Γ(G, S) be the Cayley graph
of G with respect to S. For a subset A ⊆ G denote by A∗ the complement G − A of A in G.
For a subset A ⊆ G, the edge boundary or the co-boundary δA of A consists of all (topological) edges of Γ connecting a vertex from A with a vertex from A∗.
Note that by definition δA = δA∗.
An ordered pair (A, A∗) is called a cut in Γ if δA is finite. A cut (A,A∗) is called essential if both the sets A and A∗ are infinite.
A subset A ⊆ G is called almost invariant if for every g∈G the symmetric difference
between A and Ag is finite. It is easy to see that (A, A∗) is a cut if and only if the sets A and A∗ are almost invariant (equivalently, if and only if the set A is almost invariant).
of G has at least one essential cut and hence e(G) > 1. Indeed, let X and Y be finite generating sets for H and K accordingly so that S = X ∪ Y is a finite generating set for G and let Γ=Γ(G,S) be the Cayley graph
of G with respect to S. Let A consist of the trivial element and all the elements of G whose normal form expressions for G = H∗K starts with a nontrivial element of H. Thus A∗ consists of all elements of G whose normal form expressions for G = H∗K starts with a nontrivial element of K. It is not hard to see that (A,A∗) is an essential cut in Γ so that e(G) > 1.
A more precise version of this argument shows that for a finitely generated group G:
Stallings' theorem shows that the converse is also true.
Then e(G) > 1 if and only if one of the following holds:
In the language of Bass-Serre theory this result can be restated as follows:
For a finitely generated group G we have e(G) > 1 if and only if G admits a nontrivial (that is, without a global fixed vertex) action
on a simplicial tree
with finite edge-stabilizers and without edge-inversions.
For the case where G is a torsion-free finitely generated group, Stallings' theorem implies that e(G) = ∞ if and only if G admits a proper free product
decomposition G = A∗B with both A and B nontrivial.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Stallings theorem about ends of groups states that a finitely generated group G has more than one end if and only if the group G admits a nontrivial decomposition as an amalgamated free product or an HNN extension
HNN extension
In mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
over a finite subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
. In the modern language of Bass–Serre theory
Bass–Serre theory
Bass–Serre theory is a part of the mathematical subject of group theory that deals with analyzing the algebraic structure of groups acting by automorphisms on simplicial trees...
the theorem says that a finitely generated group G has more than one end if and only if G admits a nontrivial (that is, without a global fixed point) action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a simplicial tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
with finite edge-stabilizers and without edge-inversions.
The theorem was proved by John R. Stallings
John R. Stallings
John Robert Stallings Jr. was a mathematician known for his seminal contributions to geometric group theory and 3-manifold topology. Stallings was a Professor Emeritus in the Department of Mathematics at the University of California at Berkeley where he had been a faculty member since 1967...
, first in the torsion-free case (1968) and then in the general case (1971).
Ends of graphs
Let Γ be a connected graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
where the degree of every vertex is finite. One can view Γ as a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
by giving it the natural structure of a one-dimensional cell complex. Then the ends of Γ are the ends of this topological space. A more explicit definition of the number of ends of a graph is presented below for completeness.
Let n ≥ 0 be a non-negative integer. The graph Γ is said to satisfy e(Γ) ≤ n if for every finite collection F of edges of Γ the graph Γ − F has at most n infinite connected components. By definition, e(Γ) = m if e(Γ) ≤ m and if for every 0 ≤ n < m the statement e(Γ) ≤ n is false. Thus e(Γ) = m if m is the smallest nonnegative integer n such that e(Γ) ≤ n. If there does not exist an integer n ≥ 0 such that e(Γ) ≤ n, put e(Γ) = ∞. The number e(Γ) is called the number of ends of Γ.
Informally, e(Γ) is the number of "connected components at infinity" of Γ. If e(Γ) = m < ∞, then for any finite set F of edges of Γ there exists a finite set K of edges of Γ with F ⊆ K such that Γ − F has exactly m infinite connected component
Connected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
s. If e(Γ) = ∞, then for any finite set F of edges of Γ and for any integer n ≥ 0 there exists a finite set K of edges of Γ with F ⊆ K such that Γ − K has at least n infinite connected components.
Ends of groups
Let G be a finitely generated group. Let S ⊆ G be a finite generating setGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of G and let Γ(G, S) be the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of G with respect to S. The number of ends of G is defined as e(G) = e(Γ(G, S)). A basic fact in the theory of ends of groups says that e(Γ(G, S)) does not depend on the choice of a finite generating set
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
S of G, so that e(G) is well-defined.
Basic facts and examples
- For any finitely generated group G we have e(G) ∈ {0, 1, 2, ∞}
- For a finitely generated group G we have e(G) = 0 if and only if G is finite.
- For the infinite cyclic group
we have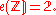 
- For the free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
of rank two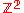
we have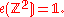 
- For a free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
F(X) where 1 < |X| < ∞ we have e(F(X)) = ∞ - For a finitely generated group G we have e(G) = 2 if and only if G is virtuallyVirtuallyIn mathematics, especially in the area of abstract algebra which studies infinite groups, the adverb virtually is used to modify a property so that it need only hold for a subgroup of finite index...
infinite cyclic (that is, G contains an infinite cyclic subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of finite indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
).
Cuts and almost invariant sets
Let G be a finitely generated group, S ⊆ G be a finite generating setGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of G and let Γ = Γ(G, S) be the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of G with respect to S. For a subset A ⊆ G denote by A∗ the complement G − A of A in G.
For a subset A ⊆ G, the edge boundary or the co-boundary δA of A consists of all (topological) edges of Γ connecting a vertex from A with a vertex from A∗.
Note that by definition δA = δA∗.
An ordered pair (A, A∗) is called a cut in Γ if δA is finite. A cut (A,A∗) is called essential if both the sets A and A∗ are infinite.
A subset A ⊆ G is called almost invariant if for every g∈G the symmetric difference
Symmetric difference
In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
between A and Ag is finite. It is easy to see that (A, A∗) is a cut if and only if the sets A and A∗ are almost invariant (equivalently, if and only if the set A is almost invariant).
Cuts and ends
A simple but important observation states:- e(G) > 1 if and only if there exists at least one essential cut (A,A∗) in Γ.
Cuts and splittings over finite groups
If G = H∗K where H and K are nontrivial finitely generated groups then the Cayley graphCayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of G has at least one essential cut and hence e(G) > 1. Indeed, let X and Y be finite generating sets for H and K accordingly so that S = X ∪ Y is a finite generating set for G and let Γ=Γ(G,S) be the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of G with respect to S. Let A consist of the trivial element and all the elements of G whose normal form expressions for G = H∗K starts with a nontrivial element of H. Thus A∗ consists of all elements of G whose normal form expressions for G = H∗K starts with a nontrivial element of K. It is not hard to see that (A,A∗) is an essential cut in Γ so that e(G) > 1.
A more precise version of this argument shows that for a finitely generated group G:
- If G = H∗CK is a free product with amalgamation where C is a finite group such that C ≠ H and C ≠ K then H and K are finitely generated and e(G) > 1 .
- If
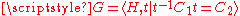is an HNN-extension where C1, C2 are isomorphic finite subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of H then G is a finitely generated group and e(G) > 1.
Stallings' theorem shows that the converse is also true.
Formal statement of Stallings' theorem
Let G be a finitely generated group.Then e(G) > 1 if and only if one of the following holds:
- The group G admits a splitting G=H∗CK as a free product with amalgamation where C is a finite group such that C ≠ H and C ≠ K.
- The group G admits a splitting
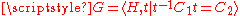is an HNN-extension where and C1, C2 are isomorphic finite subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of H.
In the language of Bass-Serre theory this result can be restated as follows:
For a finitely generated group G we have e(G) > 1 if and only if G admits a nontrivial (that is, without a global fixed vertex) action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a simplicial tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
with finite edge-stabilizers and without edge-inversions.
For the case where G is a torsion-free finitely generated group, Stallings' theorem implies that e(G) = ∞ if and only if G admits a proper free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
decomposition G = A∗B with both A and B nontrivial.
Applications and generalizations
- Among the immediate applications of Stallings' theorem was a proof by Stallings of a long-standing conjecture that every finitely generated group of cohomological dimension one is free and that every torsion-free virtuallyVirtuallyIn mathematics, especially in the area of abstract algebra which studies infinite groups, the adverb virtually is used to modify a property so that it need only hold for a subgroup of finite index...
free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
is free. - Stallings' theorem also implies that the property of having a nontrivial splitting over a finite subgroup is a quasi-isometryQuasi-isometryIn mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
invariant of a finitely generated group since the number of ends of a finitely generated group is easily seen to be a quasi-isometry invariant. For this reason Stallings' theorem is considered to be one of the first results in geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
. - Stallings' theorem was a starting point for Dunwoody's accessibility theory. A finitely generated group G is said to be accessible if the process of iterated nontrivial splitting of G over finite subgroups always terminates in a finite number of steps. In Bass-Serre theory terms that the number of edges in a reduced splitting of G as the fundamental group of a graph of groupsGraph of groupsIn geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
with finite edge groups is bounded by some constant depending on G. DunwoodyMartin DunwoodyMartin John Dunwoody is an Emeritus Professor of mathematics at the University of Southampton, England.He earned his Ph.D. in 1964 from the Australian National University. He held positions at the University of Sussex before becoming full Professor at the University of Southampton in 1992...
proved that every finitely presented group is accessible but that there do exist finitely generated groups that are not accessible. Linnell showed that if one bounds the size of finite subgroups over which the splittings are taken then every finitely generated group is accessible in this sense as well. These results in turn gave rise to other versions of accessibility such as BestvinaMladen BestvinaMladen Bestvina is a Croatian American mathematician working in the area of geometric group theory. He is a Distinguished Professor in the Department of Mathematics at the University of Utah.-Biographical info:...
-Feighn accessibility of finitely presented groups (where the so-called "small" splittings are considered), acylindrical accessibility, strong accessibility, and others. - Stallings' theorem is a key tool in proving that a finitely generated group G is virtuallyVirtuallyIn mathematics, especially in the area of abstract algebra which studies infinite groups, the adverb virtually is used to modify a property so that it need only hold for a subgroup of finite index...
freeFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
if and only if G can be represented as the fundamental group of a finite graph of groupsGraph of groupsIn geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
where all vertex and edge groups are finite (see, for example,). - Using Dunwoody's accessibility result, Stallings' theorem about ends of groups and the fact that if G is a finitely presented group with asymptotic dimension 1 then G is virtually free one can show that for a finitely presented word-hyperbolic group G the hyperbolic boundary of G has topological dimension zero if and only if G is virtually free.
- Relative versions of Stallings' theorem and relative ends of finitely generated groups with respect to subgroups have also been considered. For a subgroup H≤G of a finitely generated group G one defines the number of relative ends e(G,H) as the number of ends of the relative Cayley graph (the Schreier coset graph) of G with respect to H. The case where e(G,H)>1 is called a semi-splitting of G over H. Early work on semi-splittings, inspired by Stallings' theorem, was done in the 1970s and 1980s by Scott, Swarup, and others. The work of Sageev and Gerasomov in the 1990s showed that for a subgroup H≤G the condition e(G,H)>1 correpsonds to the group G admitting an essential isometric action on a CAT(0)-cubing where a subgroup commensurable with H stabilizes an essential "hyperplane" (a simplicial tree is an example of a CAT(0)-cubing where the hyperplanes are the midpoints of edges). In certain situations such a semi-splitting can be promoted to an actual algebraic splitting, typically over a subgroup commensurable with H, such as for the case where H is finite (Stallings' theorem). Another situation where an actual splitting can be obtained (modulo a few exceptions) is for semi-splittings over virtually polycyclicPolycyclic groupIn mathematics, a polycyclic group is a solvable group that satisfies the maximal condition on subgroups...
subgroups. Here the case of semi-splittings of word-hyperbolic groups over two-ended (virtually infinite cyclic) subgroups was treated by Scott-Swarup and by BowditchBrian BowditchBrian Hayward Bowditch is a British mathematician known for his contributions to geometry and topology, particularly in the areas of geometric group theory and low-dimensional topology. He is also known for solving the angel problem...
. The case of semi-splittings of finitely generated groups with respect to virtually polycyclic subgroups is dealt with by the algebraic torus theorem of Dunwoody-Swenson.
- A number of new proofs of Stallings' theorem have been obtained by others after Stallings' original proof. DunwoodyMartin DunwoodyMartin John Dunwoody is an Emeritus Professor of mathematics at the University of Southampton, England.He earned his Ph.D. in 1964 from the Australian National University. He held positions at the University of Sussex before becoming full Professor at the University of Southampton in 1992...
gave a proof based on the ideas of edge-cuts. Later Dunwoody also gave a proof of Stallings' theorem for finitely presented groups using the method of "tracks" on finite 2-complexes. Niblo obtained a proof of Stallings' theorem as a consequence of Sageev's CAT(0)-cubing relative version, where the CAT(0)-cubing is eventually promoted to being a tree. Niblo's paper also defines an abstract group-theoretic obstruction (which is a union of double cosets of H in G) for obtaining an actual splitting from a semi-splitting. It is also possible to prove Stallings' theorem for finitely presented groups using Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
techniques of minimal surfaceMinimal surfaceIn mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
s, where one first realizes a finitely presented group as the fundamental group of a compact 4-manifold (see, for example, a sketch of this argument in the survey article of Wall). Gromov outlined a proof (see pp. 228–230 in ) where the minimal surfaces argument is replaced by an easier harmonic analysis argument and this approach was pushed further by Kapovich to cover the original case of finitely generated groups.
See also
- Free product with amalgamation
- HNN extensionHNN extensionIn mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
- Bass-Serre theory
- Graph of groupsGraph of groupsIn geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
- Geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...