Karp-Flatt metric
Encyclopedia
The Karp–Flatt metric is a measure of parallelization of code in parallel processor systems. This metric exists in addition to Amdahl's law
and the Gustafson's law
as an indication of the extent to which a particular computer code is parallelized. It was proposed by Alan H. Karp and Horace P. Flatt in 1990.
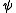on 
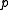processors, where 
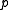> 1, the experimentally determined serial fraction 
is defined to be the Karp–Flatt Metric viz:
= 
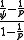
The less the value of
the better the parallelization.
running on a parallel processor. The Karp–Flatt metric defines a metric which reveals aspects of the performance that are not easily discerned from other metrics. A pseudo-"derivation" of sorts follows from Amdahl's Law
, which can be written as:
= 
+ 
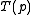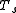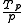
Where:
with the result obtained by substituting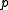
= 1 viz. 
= 
+ 
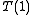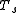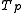, if we define the serial fraction 
= 
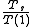then the equation can be rewritten as
= 
+ 
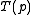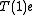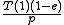
In terms of the speedup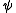
= 
:
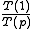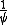= e +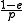 
Solving for the serial fraction, we get the Karp–Flatt metric as above.Note that this is not a "derivation" from Amdahl's law as the left hand side represents a metric
rather than a mathematically derived quantity. The treatment above merely shows that the Karp–Flatt metric is consistent with Amdahl's Law.
literature, it was rarely used as a diagnostic tool the way speedup and efficiency
are. Karp and Flatt hoped to correct this by proposing this metric. This metric addresses the inadequacies of the other laws and quantities used to measure the parallelization of computer code. In particular, Amdahl's law does not take into account load balancing
issues, nor does it take overhead
into consideration. Using the serial fraction as a metric poses definite advantages over the others, particularly as the number of processors grows.
For a problem of fixed size, the efficiency of a parallel computation typically decreases as the number of processors increases. By using the serial fraction obtained experimentally using the Karp–Flatt metric, we can determine if the efficiency decrease is due to limited opportunities of parallelism or increases in algorithmic or architectural overhead.
Amdahl's law
Amdahl's law, also known as Amdahl's argument, is named after computer architect Gene Amdahl, and is used to find the maximum expected improvement to an overall system when only part of the system is improved...
and the Gustafson's law
Gustafson's law
Gustafson's Law is a law in computer science which says that problems with large, repetitive data sets can be efficiently parallelized. Gustafson's Law contradicts Amdahl's law, which describes a limit on the speed-up that parallelization can provide. Gustafson's law was first described by John...
as an indication of the extent to which a particular computer code is parallelized. It was proposed by Alan H. Karp and Horace P. Flatt in 1990.
Description
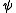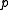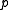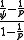
Given a parallel computation exhibiting speedup on processors, where > 1, the experimentally determined serial fraction is defined to be the Karp–Flatt Metric viz: = The less the value of
the better the parallelization.Justification
There are many ways to measure the performance of a parallel algorithmParallel algorithm
In computer science, a parallel algorithm or concurrent algorithm, as opposed to a traditional sequential algorithm, is an algorithm which can be executed a piece at a time on many different processing devices, and then put back together again at the end to get the correct result.Some algorithms...
running on a parallel processor. The Karp–Flatt metric defines a metric which reveals aspects of the performance that are not easily discerned from other metrics. A pseudo-"derivation" of sorts follows from Amdahl's Law
Amdahl's law
Amdahl's law, also known as Amdahl's argument, is named after computer architect Gene Amdahl, and is used to find the maximum expected improvement to an overall system when only part of the system is improved...
, which can be written as:
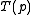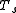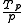
= + Where:
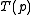is the total time taken for code execution in a 
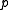-processor system
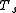is the time taken for the serial part of the code to run
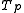is the time taken for the parallel part of the code to run in one processor
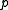is the number of processors
with the result obtained by substituting
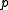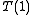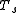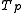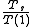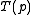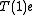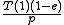
= 1 viz. = + , if we define the serial fraction = then the equation can be rewritten as = + In terms of the speedup
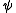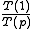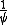= : = e + 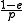Solving for the serial fraction, we get the Karp–Flatt metric as above.Note that this is not a "derivation" from Amdahl's law as the left hand side represents a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
rather than a mathematically derived quantity. The treatment above merely shows that the Karp–Flatt metric is consistent with Amdahl's Law.
Use
While the serial fraction e is often mentioned in computer scienceComputer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
literature, it was rarely used as a diagnostic tool the way speedup and efficiency
Algorithmic efficiency
In computer science, efficiency is used to describe properties of an algorithm relating to how much of various types of resources it consumes. Algorithmic efficiency can be thought of as analogous to engineering productivity for a repeating or continuous process, where the goal is to reduce...
are. Karp and Flatt hoped to correct this by proposing this metric. This metric addresses the inadequacies of the other laws and quantities used to measure the parallelization of computer code. In particular, Amdahl's law does not take into account load balancing
Load balancing (computing)
Load balancing is a computer networking methodology to distribute workload across multiple computers or a computer cluster, network links, central processing units, disk drives, or other resources, to achieve optimal resource utilization, maximize throughput, minimize response time, and avoid...
issues, nor does it take overhead
Computational overhead
In computer science, overhead is generally considered any combination of excess or indirect computation time, memory, bandwidth, or other resources that are required to attain a particular goal...
into consideration. Using the serial fraction as a metric poses definite advantages over the others, particularly as the number of processors grows.
For a problem of fixed size, the efficiency of a parallel computation typically decreases as the number of processors increases. By using the serial fraction obtained experimentally using the Karp–Flatt metric, we can determine if the efficiency decrease is due to limited opportunities of parallelism or increases in algorithmic or architectural overhead.
External links
- Lecture Notes on Karp–Flatt metric - Virginia Tech