Kerala School
Encyclopedia
The Kerala school of astronomy and mathematics was a school of mathematics
and astronomy founded by Madhava of Sangamagrama
in Kerala
, India, which included among its members: Parameshvara
, Neelakanta Somayaji, Jyeshtadeva
, Achyuta Pisharati
, Melpathur Narayana Bhattathiri
and Achyuta Panikkar
. The school flourished between the 14th and 16th centuries and the original discoveries of the school seems to have ended with Narayana Bhattathiri
(1559–1632). In attempting to solve astronomical problems, the Kerala school independently created a number of important mathematics concepts. Their most important results—series expansion for trigonometric functions—were described in Sanskrit
verse in a book by Neelakanta called Tantrasangraha, and again in a commentary on this work, called Tantrasangraha-vakhya, of unknown authorship. The theorems were stated without proof, but proofs for the series for sine, cosine, and inverse tangent were provided a century later in the work Yuktibhasa
(c.1500-c.1610), written in Malayalam, by Jyesthadeva, and also in a commentary on Tantrasangraha.
Their remarkable work, completed two centuries before the invention of calculus
in Europe, provided what is now considered the first example of a power series (apart from geometric series). However, they did not formulate a systematic theory of differentiation
and integration
, nor is there any direct evidence of their results being transmitted outside Kerala
.
and calculus
. These include the following (infinite) geometric series:
for 
This formula, however, was already known in the work of the 10th century Iraq
i mathematician
Alhazen (the Latin
ized form of the name Ibn al-Haytham) (965-1039).
The Kerala school made intuitive use of mathematical induction
, though the inductive hypothesis was not yet formulated or employed in proofs. They used this to discover a semi-rigorous proof of the result:
for large n. This result was also known to Alhazen.
They applied ideas from (what was to become) differential
and integral
calculus
to obtain (Taylor-Maclaurin
) infinite series for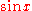
, 
, and 
. The Tantrasangraha-vakhya gives the series in verse, which when translated to mathematical notation, can be written as: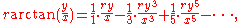
where 
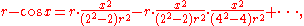where, for 
, the series reduce to the standard power series for these trigonometric functions, for example:
The Kerala school made use of the rectification (computation of length) of the arc of a circle to give a proof of these results. (The later method of Leibniz, using quadrature (i.e. computation of area under the arc of the circle), was not yet developed.) They also made use of the series expansion of
to obtain an infinite series expression (later known as Gregory series) for 
:
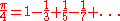
Their rational approximation of the error for the finite sum of their series are of particular interest. For example, the error,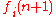
, (for n odd, and i = 1, 2, 3) for the series: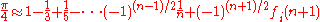
They manipulated the error term to derive a faster converging series for
:
They used the improved series to derive a rational expression,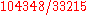
for 
correct up to nine decimal places, i.e. 
. They made use of an intuitive notion of a limit
to compute these results. The Kerala school mathematicians also gave a semi-rigorous method of differentiation of some trigonometric functions, though the notion of a function, or of exponential or logarithmic functions, was not yet formulated.
The works of the Kerala school were first written up for the Western world by Englishman C. M. Whish in 1835, though there exists some other works, namely Kala Sankalita by J.Warren in 1825 which briefly mentions the discovery of infinite series by Kerala astronomers . According to Whish, the Kerala mathematicians had "laid the foundation for a complete system of fluxions" and these works abounded "with fluxional forms and series to be found in no work of foreign countries."
However, Whish's results were almost completely neglected, until over a century later, when the discoveries of the Kerala school were investigated again by C. Rajagopal and his associates. Their work includes commentaries on the proofs of the arctan series in Yuktibhasa given in two papers, a commentary on the Yuktibhasas proof of the sine and cosine series and two papers that provide the Sanskrit
verses of the Tantrasangrahavakhya for the series for arctan, sin, and cosine (with English translation and commentary).
by traders and Jesuit missionaries. Kerala was in continuous contact with China
and Arabia, and Europe
. The suggestion of some communication routes and a chronology by some scholars could make such a transmission a possibility, however, there is no direct evidence by way of relevant manuscripts that such a transmission took place. In fact, according to David Bressoud, "there is no evidence that the Indian work of series was known beyond India, or even outside of Kerala, until the nineteenth century."
Both Arab
and Indian scholars made discoveries before the 17th century that are now considered a part of calculus. However, they were not able, as Newton
and Leibniz
were, to "combine many differing ideas under the two unifying themes of the derivative
and the integral
, show the connection between the two, and turn calculus into the great problem-solving tool we have today." The intellectual careers of both Newton and Leibniz are well-documented and there is no indication of their work not being their own; however, it is not known with certainty whether the immediate predecessors of Newton and Leibniz, "including, in particular, Fermat and Roberval, learned of some of the ideas of the Islamic and Indian mathematicians through sources of which we are not now aware." This is an active area of current research, especially in the manuscript collections of Spain
and Maghreb
, research that is now being pursued, among other places, at the Centre national de la recherche scientifique
in Paris
.
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
and astronomy founded by Madhava of Sangamagrama
Madhava of Sangamagrama
Mādhava of Sañgamāgrama was a prominent Kerala mathematician-astronomer from the town of Irińńālakkuţa near Cochin, Kerala, India. He is considered the founder of the Kerala School of Astronomy and Mathematics...
in Kerala
Kerala
or Keralam is an Indian state located on the Malabar coast of south-west India. It was created on 1 November 1956 by the States Reorganisation Act by combining various Malayalam speaking regions....
, India, which included among its members: Parameshvara
Parameshvara
Vatasseri Parameshvara Nambudiri was a major Indian mathematician and astronomer of the Kerala school of astronomy and mathematics founded by Madhava of Sangamagrama. He was also an astrologer...
, Neelakanta Somayaji, Jyeshtadeva
Jyeshtadeva
Jyeṣṭhadeva was an astronomer-mathematician of the Kerala school of astronomy and mathematics founded by Sangamagrama Madhava . He is best known as the author of Yuktibhāṣā,...
, Achyuta Pisharati
Achyuta Pisharati
Acyuta Piṣāraṭi was an Sanskrit grammarian, astrologer, astronomer and mathematician who studied under Jyeṣṭhadeva and was a member of Mādhava of Sañgamāgrama's Kerala school of astronomy and mathematics...
, Melpathur Narayana Bhattathiri
Melpathur Narayana Bhattathiri
Melpathur Narayana Bhattathiri , third student of Achyuta Pisharati, was of Madhava of Sangamagrama's Kerala school of astronomy and mathematics. He was a mathematical linguist . His most important scholarly work, Prkriya-sarvawom, sets forth an axiomatic system elaborating on the classical system...
and Achyuta Panikkar
Achyuta Panikkar
Achyuta Panikkar, was an astronomer of the Kerala school founded by Madhava of Sangamagrama. He lived between the 14th and 16th centuries.-See also:*Kerala School*Indian mathematics*Indian mathematicians...
. The school flourished between the 14th and 16th centuries and the original discoveries of the school seems to have ended with Narayana Bhattathiri
Melpathur Narayana Bhattathiri
Melpathur Narayana Bhattathiri , third student of Achyuta Pisharati, was of Madhava of Sangamagrama's Kerala school of astronomy and mathematics. He was a mathematical linguist . His most important scholarly work, Prkriya-sarvawom, sets forth an axiomatic system elaborating on the classical system...
(1559–1632). In attempting to solve astronomical problems, the Kerala school independently created a number of important mathematics concepts. Their most important results—series expansion for trigonometric functions—were described in Sanskrit
Sanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
verse in a book by Neelakanta called Tantrasangraha, and again in a commentary on this work, called Tantrasangraha-vakhya, of unknown authorship. The theorems were stated without proof, but proofs for the series for sine, cosine, and inverse tangent were provided a century later in the work Yuktibhasa
Yuktibhasa
Yuktibhāṣā also known as Gaṇitanyāyasaṅgraha , is a major treatise on mathematics and astronomy, written by Indian astronomer Jyesthadeva of the Kerala school of mathematics in about AD 1530...
(c.1500-c.1610), written in Malayalam, by Jyesthadeva, and also in a commentary on Tantrasangraha.
Their remarkable work, completed two centuries before the invention of calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
in Europe, provided what is now considered the first example of a power series (apart from geometric series). However, they did not formulate a systematic theory of differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, nor is there any direct evidence of their results being transmitted outside Kerala
Kerala
or Keralam is an Indian state located on the Malabar coast of south-west India. It was created on 1 November 1956 by the States Reorganisation Act by combining various Malayalam speaking regions....
.
Infinite Series and Calculus
The Kerala school has made a number of contributions to the fields of infinite seriesSeries (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
and calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. These include the following (infinite) geometric series:
for This formula, however, was already known in the work of the 10th century Iraq
Iraq
Iraq ; officially the Republic of Iraq is a country in Western Asia spanning most of the northwestern end of the Zagros mountain range, the eastern part of the Syrian Desert and the northern part of the Arabian Desert....
i mathematician
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
Alhazen (the Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
ized form of the name Ibn al-Haytham) (965-1039).
The Kerala school made intuitive use of mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, though the inductive hypothesis was not yet formulated or employed in proofs. They used this to discover a semi-rigorous proof of the result:
for large n. This result was also known to Alhazen.They applied ideas from (what was to become) differential
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
to obtain (Taylor-Maclaurin
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
) infinite series for
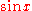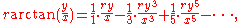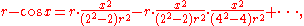, , and . The Tantrasangraha-vakhya gives the series in verse, which when translated to mathematical notation, can be written as: where where, for , the series reduce to the standard power series for these trigonometric functions, for example:
-
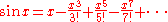and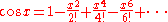
(The Kerala school themselves did not use the "factorial" symbolism.)
The Kerala school made use of the rectification (computation of length) of the arc of a circle to give a proof of these results. (The later method of Leibniz, using quadrature (i.e. computation of area under the arc of the circle), was not yet developed.) They also made use of the series expansion of
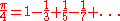
to obtain an infinite series expression (later known as Gregory series) for :Their rational approximation of the error for the finite sum of their series are of particular interest. For example, the error,
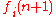, (for n odd, and i = 1, 2, 3) for the series: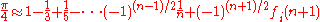
-
- where
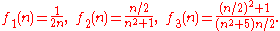
- where
They manipulated the error term to derive a faster converging series for
:They used the improved series to derive a rational expression,
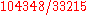for correct up to nine decimal places, i.e. . They made use of an intuitive notion of a limitLimit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
to compute these results. The Kerala school mathematicians also gave a semi-rigorous method of differentiation of some trigonometric functions, though the notion of a function, or of exponential or logarithmic functions, was not yet formulated.
The works of the Kerala school were first written up for the Western world by Englishman C. M. Whish in 1835, though there exists some other works, namely Kala Sankalita by J.Warren in 1825 which briefly mentions the discovery of infinite series by Kerala astronomers . According to Whish, the Kerala mathematicians had "laid the foundation for a complete system of fluxions" and these works abounded "with fluxional forms and series to be found in no work of foreign countries."
However, Whish's results were almost completely neglected, until over a century later, when the discoveries of the Kerala school were investigated again by C. Rajagopal and his associates. Their work includes commentaries on the proofs of the arctan series in Yuktibhasa given in two papers, a commentary on the Yuktibhasas proof of the sine and cosine series and two papers that provide the Sanskrit
Sanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
verses of the Tantrasangrahavakhya for the series for arctan, sin, and cosine (with English translation and commentary).
Possibility of transmission of Kerala School results to Europe
A. K. Bag suggested in 1979 that knowledge of these results might have been transmitted to Europe through the trade route from KeralaKerala
or Keralam is an Indian state located on the Malabar coast of south-west India. It was created on 1 November 1956 by the States Reorganisation Act by combining various Malayalam speaking regions....
by traders and Jesuit missionaries. Kerala was in continuous contact with China
China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
and Arabia, and Europe
Europe
Europe is, by convention, one of the world's seven continents. Comprising the westernmost peninsula of Eurasia, Europe is generally 'divided' from Asia to its east by the watershed divides of the Ural and Caucasus Mountains, the Ural River, the Caspian and Black Seas, and the waterways connecting...
. The suggestion of some communication routes and a chronology by some scholars could make such a transmission a possibility, however, there is no direct evidence by way of relevant manuscripts that such a transmission took place. In fact, according to David Bressoud, "there is no evidence that the Indian work of series was known beyond India, or even outside of Kerala, until the nineteenth century."
Both Arab
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
and Indian scholars made discoveries before the 17th century that are now considered a part of calculus. However, they were not able, as Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
were, to "combine many differing ideas under the two unifying themes of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, show the connection between the two, and turn calculus into the great problem-solving tool we have today." The intellectual careers of both Newton and Leibniz are well-documented and there is no indication of their work not being their own; however, it is not known with certainty whether the immediate predecessors of Newton and Leibniz, "including, in particular, Fermat and Roberval, learned of some of the ideas of the Islamic and Indian mathematicians through sources of which we are not now aware." This is an active area of current research, especially in the manuscript collections of Spain
Spain
Spain , officially the Kingdom of Spain languages]] under the European Charter for Regional or Minority Languages. In each of these, Spain's official name is as follows:;;;;;;), is a country and member state of the European Union located in southwestern Europe on the Iberian Peninsula...
and Maghreb
Maghreb
The Maghreb is the region of Northwest Africa, west of Egypt. It includes five countries: Morocco, Algeria, Tunisia, Libya, and Mauritania and the disputed territory of Western Sahara...
, research that is now being pursued, among other places, at the Centre national de la recherche scientifique
Centre national de la recherche scientifique
The National Center of Scientific Research is the largest governmental research organization in France and the largest fundamental science agency in Europe....
in Paris
Paris
Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...
.
External links
- The Kerala School, European Mathematics and Navigation, 2001.
- An overview of Indian mathematics, MacTutor History of Mathematics archiveMacTutor History of Mathematics archiveThe MacTutor History of Mathematics archive is a website maintained by John J. O'Connor and Edmund F. Robertson and hosted by the University of St Andrews in Scotland...
, 2002. - Indian Mathematics: Redressing the balance, MacTutor History of Mathematics archive, 2002.
- Keralese mathematics, MacTutor History of Mathematics archive, 2002.
- Possible transmission of Keralese mathematics to Europe, MacTutor History of Mathematics archive, 2002.
- Neither Newton nor Leibnitz - The Pre-History of Calculus and Celestial Mechanics in Medieval Kerala, 2005.
- "Indians predated Newton 'discovery' by 250 years" phys.org, 2007
See also
- Indian astronomy
- Indian mathematicsIndian mathematicsIndian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
- Indian mathematicians
- History of mathematicsHistory of mathematicsThe area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....