
Killing tensor
Encyclopedia
A Killing tensor, named after Wilhelm Killing
, is a tensor
, known in the theory of general relativity
, that satisfies
that satisfies
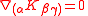
where the parentheses on the indices refer to the symmetric part.
This is a generalization of a Killing vector. While Killing vectors are associated with continuous symmetries (more precisely, differentiable), and hence very common, the concept of Killing tensor arises much less frequently. The Kerr solution
is the most famous example of a manifold possessing a Killing tensor.
Wilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
, is a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, known in the theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
,
 that satisfies
that satisfies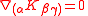
where the parentheses on the indices refer to the symmetric part.
This is a generalization of a Killing vector. While Killing vectors are associated with continuous symmetries (more precisely, differentiable), and hence very common, the concept of Killing tensor arises much less frequently. The Kerr solution
Kerr metric
The Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
is the most famous example of a manifold possessing a Killing tensor.

