Symmetric tensor
Encyclopedia
In mathematics
, a symmetric tensor is tensor
that is invariant under a permutation
of its vector arguments. Thus an rth order symmetric tensor represented in coordinates as a quantity with r indices satisfies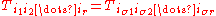
for every permutation σ of the symbols {1,2,...,r}.
The space of symmetric tensors of rank r on a finite dimensional vector space
is naturally isomorphic to the dual of the space of homogeneous polynomial
s of degree r on V. Over fields
of characteristic zero, the graded vector space
of all symmetric tensors can be naturally identified with the symmetric algebra
on V. A related concept is that of the antisymmetric tensor or alternating form. Symmetric tensors occur widely in engineering
, physics
and mathematics
.
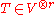
a tensor of order r. Then T is a symmetric tensor if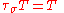
for the braiding maps associated to every permutation σ on the symbols {1,2,...,r} (or equivalently for every transposition
on these symbols).
Given a basis
{ei} of V, any symmetric tensor T of rank r can be written as
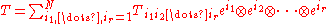
for some unique list of coefficients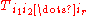
(the components of the tensor in the basis) that are symmetric on the indices. That is to say
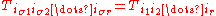
for every permutation
σ.
The space of all symmetric tensors of rank r defined on V is often denoted by Sr(V) or Symr(V). It is itself a vector space, and if V has dimension N then the dimension of Symr(V) is the binomial coefficient
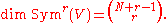
is a vector space over a field of characteristic
0. If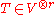
is a tensor of order 
, then the symmetric part of 
is the symmetric tensor defined by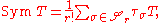
the summation extending over the symmetric group
on r symbols. In terms of a basis, and employing the Einstein summation convention, if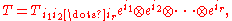
then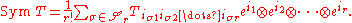
The components of the tensor appearing on the right are often denoted by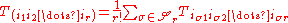
with parentheses around the indices which have been symmetrized. [Square brackets are used to indicate anti-symmetrization.]
If T is a simple tensor, given as a pure tensor product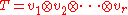
then the symmetric part of T is the symmetric product of the factors:
used in physics and engineering can be represented as symmetric tensor fields; for example, stress
, strain, and anisotropic conductivity
.
In full analogy with the theory of symmetric matrices, a (real) symmetric tensor of order 2 can be "diagonalized". More precisely, for any tensor T ∈ Sym2(V), there is an integer n and non-zero vectors v1,...,vn ∈ V such that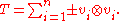
This is Sylvester's law of inertia
. The minimum number n for which such a decomposition is possible is the rank of T. The vectors appearing in this minimal expression are the principal axes of the tensor, and generally have an important physical meaning. For example, the principal axes of the inertia tensor define the ellipsoid representing the moment of inertia.
Ellipsoids are examples of algebraic varieties; and so, for general rank, symmetric tensors, in the guise of homogeneous polynomial
s, are used to define projective varieties, and are often studied as such.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a symmetric tensor is tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
that is invariant under a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of its vector arguments. Thus an rth order symmetric tensor represented in coordinates as a quantity with r indices satisfies
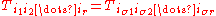
for every permutation σ of the symbols {1,2,...,r}.
The space of symmetric tensors of rank r on a finite dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is naturally isomorphic to the dual of the space of homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s of degree r on V. Over fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic zero, the graded vector space
Graded vector space
In mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
of all symmetric tensors can be naturally identified with the symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
on V. A related concept is that of the antisymmetric tensor or alternating form. Symmetric tensors occur widely in engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
.
Definition
Let V be a vector space and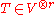a tensor of order r. Then T is a symmetric tensor if
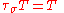
for the braiding maps associated to every permutation σ on the symbols {1,2,...,r} (or equivalently for every transposition
Transposition
Transposition may refer to:Mathematics* Transposition , a permutation which exchanges two elements and keeps all others fixed* Transposition, producing the transpose of a matrix AT, which is computed by swapping columns for rows in the matrix AGames* Transposition , different moves or a different...
on these symbols).
Given a basis
Basis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
{ei} of V, any symmetric tensor T of rank r can be written as
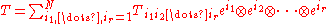
for some unique list of coefficients
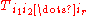(the components of the tensor in the basis) that are symmetric on the indices. That is to say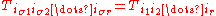for every permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
σ.
The space of all symmetric tensors of rank r defined on V is often denoted by Sr(V) or Symr(V). It is itself a vector space, and if V has dimension N then the dimension of Symr(V) is the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
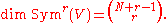
Symmetric part of a tensor
Suppose is a vector space over a field of characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0. If
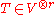is a tensor of order , then the symmetric part of is the symmetric tensor defined by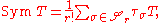the summation extending over the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on r symbols. In terms of a basis, and employing the Einstein summation convention, if
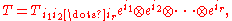
then
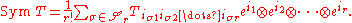
The components of the tensor appearing on the right are often denoted by
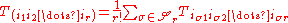
with parentheses around the indices which have been symmetrized. [Square brackets are used to indicate anti-symmetrization.]
If T is a simple tensor, given as a pure tensor product
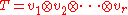
then the symmetric part of T is the symmetric product of the factors:
Examples
Many material properties and fieldsField (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
used in physics and engineering can be represented as symmetric tensor fields; for example, stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
, strain, and anisotropic conductivity
Conductivity
Conductivity may refer to:*Electrical conductivity, a measure of a material's ability to conduct an electric current*Conductivity , also the specific conductance, is a measurement of the electrical conductance per unit distance in an electrolytic or aqueous solution*Ionic conductivity, a measure of...
.
In full analogy with the theory of symmetric matrices, a (real) symmetric tensor of order 2 can be "diagonalized". More precisely, for any tensor T ∈ Sym2(V), there is an integer n and non-zero vectors v1,...,vn ∈ V such that
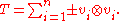
This is Sylvester's law of inertia
Sylvester's law of inertia
Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of coordinates...
. The minimum number n for which such a decomposition is possible is the rank of T. The vectors appearing in this minimal expression are the principal axes of the tensor, and generally have an important physical meaning. For example, the principal axes of the inertia tensor define the ellipsoid representing the moment of inertia.
Ellipsoids are examples of algebraic varieties; and so, for general rank, symmetric tensors, in the guise of homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s, are used to define projective varieties, and are often studied as such.
See also
- antisymmetric tensor
- transposeTransposeIn linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
- symmetric polynomialSymmetric polynomialIn mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
- Schur polynomialSchur polynomialIn mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
- Young symmetrizerYoung symmetrizerIn mathematics, a Young symmetrizer is an element of the group algebra of the symmetric group, constructed in such a way that the image of the element corresponds to an irreducible representation of the symmetric group over the complex numbers. A similar construction works over any field, and the...
External links
- Cesar O. Aguilar, The Dimension of Symmetric k-tensors