Kleene's T predicate
Encyclopedia
In computability theory
, the T predicate, first studied by mathematician Stephen Cole Kleene
, is a particular set of triples of natural number
s that is used to represent computable function
s within formal theories
of arithmetic
. Informally, the T predicate tells whether a particular computer program
will halt when run with a particular input, and the corresponding U function is used to obtain the results of the computation if the program does halt. As with the smn theorem, the original notation used by Kleene has become standard terminology for the concept.
s. This numbering must be sufficiently effective that, given an index of a computable function and an input to the function, it is possible to effectively simulate the computation of the function on that input. The T predicate is obtained by formalizing this simulation.
The ternary relation T1(e,i,x) takes three natural numbers as arguments. The triples of numbers (e,i,x) that belong to the relation (the ones for which T1(e,i,x) is true) are defined to be exactly the triples in which x encodes a computation history of the computable function with index e when run with input i, and the program halts as the last step of this computation history. That is, T1 first asks whether x is the Gödel number
of a finite sequence ⟨xj⟩ of complete configurations of the Turing machine with index e, running a computation on input i. If so, T1 then asks if this sequence begins with the starting state of the computation and each successive element of the sequence corresponds to a single step of the Turing machine. If it does, T1 finally asks whether the sequence ⟨xj⟩ ends with the machine in a halting state. If all three of these questions have a positive answer, then T1(e,i,x) holds (is true). Otherwise, T1(e,i,x) does not hold (is false).
There is a corresponding function U such that if T(e,i,x) holds then U(x) returns the output of the function with index e on input i.
Because Kleene's formalism attaches a number of inputs to each function, the predicate T1 can only be used for functions that take one input. There are additional predicates for functions with multiple inputs; the relation
,
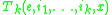holds if x encodes a halting computation of the function with index e on the inputs i1,...,ik.
,
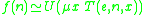where μ is the μ operator
and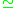
holds if both sides are undefined or if both are defined and they are equal.
Because of this, any theory of arithmetic that is able to represent every primitive recursive function is able to represent T and U. Examples of such arithmetical theories include Robinson arithmetic
and stronger theories such as Peano arithmetic.
. In particular, the set
which is of the same Turing degree
as the halting problem
, is a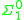
complete unary relation (Soare 1987, pp. 28, 41). More generally, the set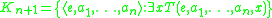
is a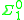
complete (n+1)-ary predicate. Thus, once a representation of the T predicate is obtained in a theory of arithmetic, a representation of a 
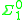-complete predicate can be obtained from it.
This construction can be extended higher in the arithmetical hierarchy, as in Post's theorem
(compare Hinman 2005, p. 397). For example, if a set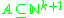
is 
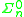complete then the set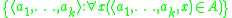
is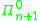
complete.
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, the T predicate, first studied by mathematician Stephen Cole Kleene
Stephen Cole Kleene
Stephen Cole Kleene was an American mathematician who helped lay the foundations for theoretical computer science...
, is a particular set of triples of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s that is used to represent computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s within formal theories
Formal theory
Formal theory can refer to:* Another name for a theory which is expressed in formal language.* An axiomatic system, something representable by symbols and its operators...
of arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
. Informally, the T predicate tells whether a particular computer program
Computer program
A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...
will halt when run with a particular input, and the corresponding U function is used to obtain the results of the computation if the program does halt. As with the smn theorem, the original notation used by Kleene has become standard terminology for the concept.
Definition
The definition depends on a suitable Gödel numbering that assigns natural numbers to computable functionComputable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s. This numbering must be sufficiently effective that, given an index of a computable function and an input to the function, it is possible to effectively simulate the computation of the function on that input. The T predicate is obtained by formalizing this simulation.
The ternary relation T1(e,i,x) takes three natural numbers as arguments. The triples of numbers (e,i,x) that belong to the relation (the ones for which T1(e,i,x) is true) are defined to be exactly the triples in which x encodes a computation history of the computable function with index e when run with input i, and the program halts as the last step of this computation history. That is, T1 first asks whether x is the Gödel number
Gödel numbering for sequences
A Gödel numbering for sequences provides us an effective way to represent each finite sequence of natural numbers as a single natural number. Of course, the embedding is surely possible set theoretically, but the emphasis is on the effectiveness of the functions manipulating such representations of...
of a finite sequence ⟨xj⟩ of complete configurations of the Turing machine with index e, running a computation on input i. If so, T1 then asks if this sequence begins with the starting state of the computation and each successive element of the sequence corresponds to a single step of the Turing machine. If it does, T1 finally asks whether the sequence ⟨xj⟩ ends with the machine in a halting state. If all three of these questions have a positive answer, then T1(e,i,x) holds (is true). Otherwise, T1(e,i,x) does not hold (is false).
There is a corresponding function U such that if T(e,i,x) holds then U(x) returns the output of the function with index e on input i.
Because Kleene's formalism attaches a number of inputs to each function, the predicate T1 can only be used for functions that take one input. There are additional predicates for functions with multiple inputs; the relation
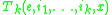,holds if x encodes a halting computation of the function with index e on the inputs i1,...,ik.
Normal form theorem
The T predicate can be used to obtain Kleene's normal form theorem for computable functions (Soare 1987, p. 15). This states that a function f(n) is computable if and only if there is an e such that for all n,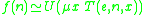,where μ is the μ operator
Mu operator
In computability theory, the μ operator, minimization operator, or unbounded search operator searches for the least natural number with a given property.- Definition :...
and
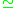holds if both sides are undefined or if both are defined and they are equal.Formalization
The T predicate is primitive recursive in the sense that there is a primitive recursive function that, given inputs for the predicate, correctly determine the truth value of the predicate on those inputs. Similarly, the U function is primitive recursive.Because of this, any theory of arithmetic that is able to represent every primitive recursive function is able to represent T and U. Examples of such arithmetical theories include Robinson arithmetic
Robinson arithmetic
In mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
and stronger theories such as Peano arithmetic.
Arithmetical hierarchy
In addition to encoding computability, the T predicate can be used to generate complete sets in the arithmetical hierarchyArithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
. In particular, the set
- K = { e : ∃ x T(e,0,x)},
which is of the same Turing degree
Turing degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
as the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
, is a
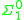complete unary relation (Soare 1987, pp. 28, 41). More generally, the set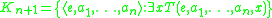is a
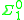complete (n+1)-ary predicate. Thus, once a representation of the T predicate is obtained in a theory of arithmetic, a representation of a 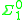-complete predicate can be obtained from it.This construction can be extended higher in the arithmetical hierarchy, as in Post's theorem
Post's theorem
In computability theory Post's theorem, named after Emil Post, describes the connection between the arithmetical hierarchy and the Turing degrees.- Background :The statement of Post's theorem uses several concepts relating to definability and recursion theory...
(compare Hinman 2005, p. 397). For example, if a set
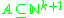is 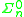complete then the set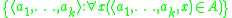is
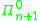complete.