
Klein transformation
Encyclopedia
In quantum field theory
, the Klein transformation is a redefinition of the fields to patch up the spin-statistics theorem
.

Also suppose χ is invariant under the Z2 parity (nothing to do with spatial reflections!) mapping χ to −χ but leaving φ invariant. Obviously, free field theories always satisfy this property. Then, the Z2 parity of the number of χ particles is well defined and is conserved in time (even though the number of χ particles itself depends on the choice of which splitting into a free Hamiltonian and an interacting Hamiltonian we make in the interaction picture
, which doesn't even exist for interacting theories (the number is typically infinite)). Let's denote this parity by the operator Kχ which maps χ-even states to itself and χ-odd states into their negative. Then, Kχ is involutive, Hermitian
and unitary
.
Needless to say, the fields φ and χ above don't have the proper statistics relations for either a boson or a fermion. i.e. they are bosonic with respect to themselves but fermionic with respect to each other. But if you look at the statistical properties alone, we find it has exactly the same statistics as the Bose–Einstein statistics. Here's why:
Define two new fields φ' and χ' as follows:
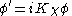
and
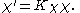
This redefinition is invertible (because Kχ is). Now, the spacelike commutation relations become
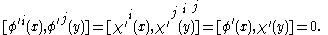
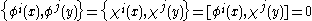
(spacelike-separated as usual).
Assume once again we have a Z2 conserved parity operator Kχ acting upon χ alone.
Let
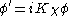
and
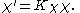
Then
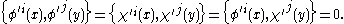
This explains the equivalence between parastatistics
and the more familiar Bose–Einstein
/Fermi–Dirac statistics.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the Klein transformation is a redefinition of the fields to patch up the spin-statistics theorem
Spin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
.
Bose–Einstein
Suppose φ and χ are fields such that, if x and y are spacelike-separated points and i and j represent the spinor/tensor indices,
Also suppose χ is invariant under the Z2 parity (nothing to do with spatial reflections!) mapping χ to −χ but leaving φ invariant. Obviously, free field theories always satisfy this property. Then, the Z2 parity of the number of χ particles is well defined and is conserved in time (even though the number of χ particles itself depends on the choice of which splitting into a free Hamiltonian and an interacting Hamiltonian we make in the interaction picture
Interaction picture
In quantum mechanics, the Interaction picture is an intermediate between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of...
, which doesn't even exist for interacting theories (the number is typically infinite)). Let's denote this parity by the operator Kχ which maps χ-even states to itself and χ-odd states into their negative. Then, Kχ is involutive, Hermitian
Hermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
and unitary
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
.
Needless to say, the fields φ and χ above don't have the proper statistics relations for either a boson or a fermion. i.e. they are bosonic with respect to themselves but fermionic with respect to each other. But if you look at the statistical properties alone, we find it has exactly the same statistics as the Bose–Einstein statistics. Here's why:
Define two new fields φ' and χ' as follows:
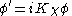
and
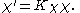
This redefinition is invertible (because Kχ is). Now, the spacelike commutation relations become
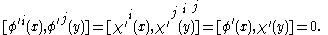
Fermi–Dirac
Now, let's work with the example where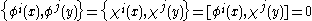
(spacelike-separated as usual).
Assume once again we have a Z2 conserved parity operator Kχ acting upon χ alone.
Let
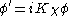
and
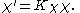
Then
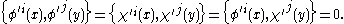
More than two fields
But what if we have more than two fields? In that case, we can keep on applying the Klein transformation to each pair of fields with the "wrong" commutation/anticommutation relations until we're done.This explains the equivalence between parastatistics
Parastatistics
In quantum mechanics and statistical mechanics, parastatistics is one of several alternatives to the better known particle statistics models...
and the more familiar Bose–Einstein
Bose–Einstein statistics
In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...
/Fermi–Dirac statistics.

