
Parastatistics
Encyclopedia
In quantum mechanics
and statistical mechanics
, parastatistics is one of several alternatives to the better known particle statistics
models (Bose–Einstein statistics
, Fermi–Dirac statistics and Maxwell–Boltzmann statistics
). Other alternatives include anyonic statistics and braid statistics
, both of these involving lower spacetime dimensions.
of a system of N identical particles. This is a *-algebra
. There is an SN group (symmetric group
of order N) acting
upon the operator algebra with the intended interpretation of permuting
the N particles. Quantum mechanics requires focus on observable
s having a physical meaning, and the observables would have to be invariant
under all possible permutations of the N particles. For example in the case N = 2, R2 − R1 cannot be an observable because it changes sign if we switch the two particles, but the distance between the two particles : |R2 − R1| is a legitimate observable.
In other words, the observable algebra would have to be a *-subalgebra
invariant under the action of SN (noting that this does not mean that every element of the operator algebra invariant under SN is an observable). Therefore we can have different superselection sector
s, each parameterized by a Young diagram of SN.
In particular:
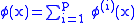 where if x and y are spacelike-separated points,
where if x and y are spacelike-separated points, 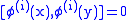 and
and 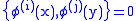 if
if  where [,] is the commutator
where [,] is the commutator
and {,} is the anticommutator. Note that this disagrees with the spin-statistics theorem
, which is for boson
s and not parabosons. There might be a group such as the symmetric group
Sp acting upon the φ(i)s. Observable
s would have to be operators which are invariant
under the group in question. However, the existence of such a symmetry is not essential.
A parafermion field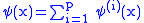 of order p, where if x and y are spacelike-separated points,
of order p, where if x and y are spacelike-separated points,  and
and 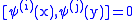 if
if  . The same comment about observable
. The same comment about observable
s would apply together with the requirement that they have even grading
under the grading where the ψs have odd grading.
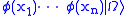
corresponds to creating n identical parabosons at x1,..., xn. Similarly,
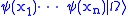
corresponds to creating n identical parafermions. Because these fields neither commute nor anticommute
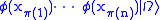
and
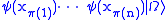
gives distinct states for each permutation π in Sn
.
We can define a permutation operator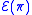 by
by
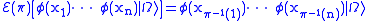
and
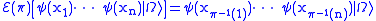
respectively. This can be shown to be well-defined as long as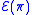 is only restricted to states spanned by the vectors given above (essentially the states with n identical particles). It is also unitary
is only restricted to states spanned by the vectors given above (essentially the states with n identical particles). It is also unitary
. Moreover, is an operator-valued representation
is an operator-valued representation
of the symmetric group Sn and as such, we can interpret it as the action of Sn upon the n-particle Hilbert space itself, turning it into a unitary representation
.
QCD
can be reformulated using parastatistics with the quarks being parafermions of order 3 and the gluons being parabosons of order 8. Note this is different from the conventional approach where quarks always obey anticommutation relations and gluons commutation relations.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, parastatistics is one of several alternatives to the better known particle statistics
Particle statistics
Particle statistics refers to the particular description of particles in statistical mechanics.-Classical statistics:In classical mechanics all the particles in the system are considered distinguishable. This means that one can label and track each individual particle in a system...
models (Bose–Einstein statistics
Bose–Einstein statistics
In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...
, Fermi–Dirac statistics and Maxwell–Boltzmann statistics
Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the statistical distribution of material particles over various energy states in thermal equilibrium, when the temperature is high enough and density is low enough to render quantum effects negligible.The expected number of particles...
). Other alternatives include anyonic statistics and braid statistics
Braid statistics
In mathematics and theoretical physics, braid statistics is a generalization of the statistics of bosons and fermions based on the concept of braid group. A similar notion exists using a loop braid group.-See also:* Braid symmetry* Parastatistics...
, both of these involving lower spacetime dimensions.
Formalism
Consider the operator algebraOperator algebra
In functional analysis, an operator algebra is an algebra of continuous linear operators on a topological vector space with the multiplication given by the composition of mappings...
of a system of N identical particles. This is a *-algebra
Star-algebra
-*-ring:In mathematics, a *-ring is an associative ring with a map * : A → A which is an antiautomorphism and an involution.More precisely, * is required to satisfy the following properties:* ^* = x^* + y^** ^* = y^* x^** 1^* = 1...
. There is an SN group (symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
of order N) acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
upon the operator algebra with the intended interpretation of permuting
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
the N particles. Quantum mechanics requires focus on observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
s having a physical meaning, and the observables would have to be invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under all possible permutations of the N particles. For example in the case N = 2, R2 − R1 cannot be an observable because it changes sign if we switch the two particles, but the distance between the two particles : |R2 − R1| is a legitimate observable.
In other words, the observable algebra would have to be a *-subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
invariant under the action of SN (noting that this does not mean that every element of the operator algebra invariant under SN is an observable). Therefore we can have different superselection sector
Superselection sector
In Quantum mechanics, superselection extends the concept of selection rules.Superselection rules are postulated rules forbidding the preparation of quantum states that exhibit coherence between eigenstates of certain observables....
s, each parameterized by a Young diagram of SN.
In particular:
- If we have N identical parabosons of order p (where p is a positive integer), then the permissible Young diagrams are all those with p or fewer rows.
- If we have N identical parafermions of order p, then the permissible Young diagrams are all those with p or fewer columns.
- If p is 1, we just have the ordinary cases of Bose–Einstein and Fermi–Dirac statistics respectively.
- If p is infinity (not an integer, but one could also have said arbitrarily large p), we have Maxwell–Boltzmann statistics.
The quantum field theory of parastatistics
A paraboson field of order p,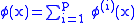 where if x and y are spacelike-separated points,
where if x and y are spacelike-separated points, 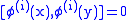 and
and 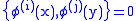 if
if  where [,] is the commutator
where [,] is the commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
and {,} is the anticommutator. Note that this disagrees with the spin-statistics theorem
Spin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
, which is for boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s and not parabosons. There might be a group such as the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sp acting upon the φ(i)s. Observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
s would have to be operators which are invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under the group in question. However, the existence of such a symmetry is not essential.
A parafermion field
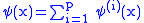 of order p, where if x and y are spacelike-separated points,
of order p, where if x and y are spacelike-separated points,  and
and 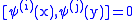 if
if  . The same comment about observable
. The same comment about observableObservable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
s would apply together with the requirement that they have even grading
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
under the grading where the ψs have odd grading.
Explaining parastatistics
Note that if x and y are spacelike-separated points, φ(x) and φ(y) neither commute nor anticommute unless p=1. The same comment applies to ψ(x) and ψ(y). So, if we have n spacelike separated points x1, ..., xn,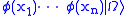
corresponds to creating n identical parabosons at x1,..., xn. Similarly,
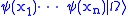
corresponds to creating n identical parafermions. Because these fields neither commute nor anticommute
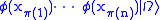
and
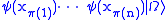
gives distinct states for each permutation π in Sn
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
.
We can define a permutation operator
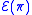 by
by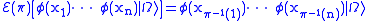
and
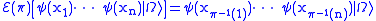
respectively. This can be shown to be well-defined as long as
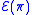 is only restricted to states spanned by the vectors given above (essentially the states with n identical particles). It is also unitary
is only restricted to states spanned by the vectors given above (essentially the states with n identical particles). It is also unitaryUnitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
. Moreover,
 is an operator-valued representation
is an operator-valued representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the symmetric group Sn and as such, we can interpret it as the action of Sn upon the n-particle Hilbert space itself, turning it into a unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
.
QCD
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
can be reformulated using parastatistics with the quarks being parafermions of order 3 and the gluons being parabosons of order 8. Note this is different from the conventional approach where quarks always obey anticommutation relations and gluons commutation relations.
History of parastatistics
H.S. (Bert) Green is credited with the invention/discovery of parastatistics in 1953See also
- Klein transformation on how to convert between parastatistics and the more conventional statistics

