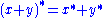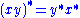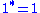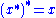Star-algebra
Encyclopedia
*-ring
In mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a *-ring is an associative ring with a map * : A → A which is an antiautomorphism and an involution
Semigroup with involution
In mathematics, in semigroup theory, an involution in a semigroup is a transformation of the semigroup which is its own inverse and which is an anti-automorphism of the semigroup. A semigroup in which an involution is defined is called a semigroup with involution...
.
More precisely, * is required to satisfy the following properties:
for all x,y in A.
This is also called an involutive ring, involutory ring, and ring with involution. Note, that the third axiom is actually redundant, because the second and fourth axioms imply
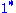 is also an identity, and identities are unique.
is also an identity, and identities are unique.Elements such that
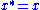 are called self-adjoint
are called self-adjointSelf-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
or Hermitian.
One can define a sesquilinear form
Sesquilinear form
In mathematics, a sesquilinear form on a complex vector space V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix sesqui- meaning "one and a half"...
over any *-ring.
*-algebra
A *-algebra A is a *-ring that is an associative algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over a commutative
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
*-ring R, with the * agreeing on
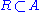 .
.The base *-ring is usually the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s (with * acting as complex conjugation) and commutes with A.
Since R is central, the * on A is conjugate-linear in R, meaning
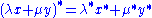
for
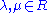 ,
, 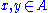 .
.A *-homomorphism
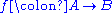 is algebra homomorphism
is algebra homomorphismAlgebra homomorphism
A homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
that is compatible with the involutions of A and B, i.e.,
-
 for all a in A.
for all a in A.
*-operation
A *-operation on a *-ring is an operation on a ring that behaves similarly to complex conjugation on the complex numbers. A *-operation on a *-algebra is an operation on an algebra over a *-ring that behaves similarly to taking adjointsConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
in
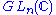 .
.Examples
- The most familiar example of a *-algebra is the field of complex numbers C where * is just complex conjugation.
- More generally, the conjugation involution in any Cayley–Dickson algebra such as the complex numbers, quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s and octonionOctonionIn mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s, if a blind eye is turned on the nonassociativity of the latter. - Another example is the matrix algebraMatrix ringIn abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
of n×n matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
over C with * given by the conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
. - Its generalization, the Hermitian adjointHermitian adjointIn mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of a linear operator on a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is also a star-algebra. - In Hecke algebraHecke algebraIn mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke and Nagayoshi Iwahori, is a one-parameter deformation of the group algebra of a Coxeter group....
, an involution is important to the Kazhdan–Lusztig polynomialKazhdan–Lusztig polynomialIn representation theory, a Kazhdan–Lusztig polynomial Py,w is a member of a family of integral polynomials introduced by . They are indexed by pairs of elements y, w of a Coxeter group W, which can in particular be the Weyl group of a Lie group.- Motivation and history:In the spring of 1978...
. - Any commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
becomes a *-ring with the trivial involution. - The endomorphism ringEndomorphism ringIn abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of an elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
becomes a *-algebra over the integers, where the involution is given by taking the dual isogenyDual abelian varietyIn mathematics, a dual abelian variety can be defined from an abelian variety A, defined over a field K.-Definition:To an abelian variety A over a field k, one associates a dual abelian variety Av , which is the solution to the following moduli problem...
. A similar construction works for abelian varietiesAbelian varietyIn mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
with a polarizationAbelian varietyIn mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
, in which case it is called the rosati involution (see Milne's lecture notes on abelian varieties).
Involutive Hopf algebras are important examples of *-algebras (with the additional structure of a compatible comultiplication); the most familiar example being:
- The group Hopf algebraGroup Hopf algebraIn mathematics, the group Hopf algebra of a given group is a certain construct related to the symmetries of group actions. Deformations of group Hopf algebras are foundational in the theory of quantum groups.-Definition:...
: a group ringGroup ringIn algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
, with involution given by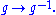
Additional structures
Many properties of the transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
hold for general *-algebras:
- The Hermitian elements form a Jordan algebraJordan algebraIn abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
; - The skew Hermitian elements form a Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
; - If 2 is invertible, then
 and
and  are orthogonal idempotents, called symmetrizing and anti-symmetrizing, so the algebra decomposes as a direct sum of symmetric and anti-symmetric (Hermitian and skew Hermitian) elements. This decomposition is as a vector space, not as an algebra, because the idempotents are operators, not elements of the algebra.
are orthogonal idempotents, called symmetrizing and anti-symmetrizing, so the algebra decomposes as a direct sum of symmetric and anti-symmetric (Hermitian and skew Hermitian) elements. This decomposition is as a vector space, not as an algebra, because the idempotents are operators, not elements of the algebra.
Skew structures
Given a *-ring, there is also the map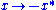 .
.This is not a *-ring structure (unless the characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
is 2, in which case it's identical to the original *), as
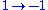 (so * is not a ring homomorphism), neither is it antimultiplicative, but it satisfies the other axioms (linear, involution) and hence is quite similar.
(so * is not a ring homomorphism), neither is it antimultiplicative, but it satisfies the other axioms (linear, involution) and hence is quite similar.Elements fixed by this map (i.e., such that
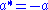 ) are called skew Hermitian.
) are called skew Hermitian.For the complex numbers with complex conjugation, the real numbers are the Hermitian elements, and the imaginary numbers are the skew Hermitian.
See also
- B*-algebra
- C*-algebra
- von Neumann algebraVon Neumann algebraIn mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
- Baer ringBaer ringIn abstract algebra and functional analysis, Baer rings, Baer *-rings, Rickart rings, Rickart *-rings, and AW* algebras are various attempts to give an algebraic analogue of von Neumann algebras, using axioms about annihilators of various sets.Any von Neumann algebra is a Baer *-ring, and much of...
- operator algebraOperator algebraIn functional analysis, an operator algebra is an algebra of continuous linear operators on a topological vector space with the multiplication given by the composition of mappings...