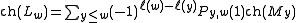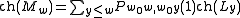Kazhdan–Lusztig polynomial
Encyclopedia
In representation theory
, a Kazhdan–Lusztig polynomial Py,w(q) is a member of a family of integral polynomials introduced by . They are indexed by pairs of elements y, w of a Coxeter group
W, which can in particular be the Weyl group
of a Lie group
.
essentially given by the Kazhdan–Lusztig polynomials. The actual Kazhdan–Lusztig construction of their polynomials is more elementary.
Kazhdan and Lusztig used this to construct a canonical basis
in the Hecke algebra
of the Coxeter group and its representations.
In their first paper Kazhdan and Lusztig mentioned that their polynomials were related to the failure of local Poincaré duality
for Schubert varieties. In they reinterpreted this in terms of the intersection cohomology
of Mark Goresky
and Robert MacPherson, and gave another definition of such a basis in terms of the dimensions of certain intersection cohomology groups.
The two bases for the Springer representation reminded Kazhdan and Lusztig of the two bases for the Grothendieck group
of certain infinite dimensional representations of semisimple Lie algebras, given by Verma module
s and simple module
s. This analogy, and the work of Jantzen
and Joseph relating primitive ideal
s of enveloping algebra
s to representations of Weyl groups, led to the Kazhdan–Lusztig conjectures.
of W has a basis of elements Tw for w∈W over the ring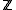 [q1/2, q−1/2], with multiplication defined by
[q1/2, q−1/2], with multiplication defined by
The Kazhdan–Lusztig polynomials Pyw(q) are indexed by a pair of elements y, w of W, and uniquely determined by the following properties.
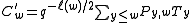
are invariant under the involution D of the Hecke algebra taking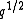 to
to  .
.
and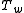 to
to 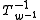 for all elements w ∈ W. The elements
for all elements w ∈ W. The elements 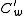 form a basis of the Hecke algebra as a
form a basis of the Hecke algebra as a  [q1/2, q−1/2]-module, called the Kazhdan–Lusztig basis.
[q1/2, q−1/2]-module, called the Kazhdan–Lusztig basis.
To establish existence of the Kazhdan–Lusztig polynomials, Kazhdan and Lusztig gave a simple recursive procedure for computing the polynomials Pyw(q) in terms of more elementary polynomials denoted Ryw(q). defined by
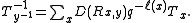
They can be computed using the recursion relations
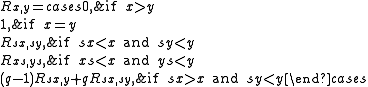
The Kazhdan–Lusztig polynomials can then be computed recursively using the relation

using the fact that the two terms on the left are polynomials in q1/2 and q−1/2 without constant term
s.
These formulas are tiresome to use by hand for rank greater than about 3, but are well adapted for computers, and the only limit on computing Kazhdan–Lusztig polynomials with them is that for large rank the number of such polynomials exceeds the storage capacity of computers.
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, a Kazhdan–Lusztig polynomial Py,w(q) is a member of a family of integral polynomials introduced by . They are indexed by pairs of elements y, w of a Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
W, which can in particular be the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
.
Motivation and history
In the spring of 1978 Kazhdan and Lusztig were studying Springer representations of the Weyl group of an algebraic group on l-adic cohomology groups related to unipotent conjugacy classes. They found a new construction of these representations over the complex numbers . The representation had two natural bases, and the transition matrix between these two bases isessentially given by the Kazhdan–Lusztig polynomials. The actual Kazhdan–Lusztig construction of their polynomials is more elementary.
Kazhdan and Lusztig used this to construct a canonical basis
Canonical basis
In mathematics, a canonical basis is a basis of an algebraic structure that is canonical in a sense that depends on the precise context:* In a coordinate space, and more generally in a free module, it refers to the standard basis defined by the Kronecker delta...
in the Hecke algebra
Hecke algebra
In mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke and Nagayoshi Iwahori, is a one-parameter deformation of the group algebra of a Coxeter group....
of the Coxeter group and its representations.
In their first paper Kazhdan and Lusztig mentioned that their polynomials were related to the failure of local Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
for Schubert varieties. In they reinterpreted this in terms of the intersection cohomology
Intersection cohomology
In topology, a branch of mathematics, intersection homology is an analogue of singular homology especially well-suited for the study of singular spaces, discovered by Mark Goresky and Robert MacPherson in the fall of 1974 and developed by them over the next few years.Intersection cohomology was...
of Mark Goresky
Mark Goresky
Robert Mark Goresky is a Canadian mathematician who invented intersection homology with Robert MacPherson.He received his Ph.D. from Brown University in 1976. His thesis, titled Geometric Cohomology and Homology of Stratified Objects, was written under the direction of MacPherson...
and Robert MacPherson, and gave another definition of such a basis in terms of the dimensions of certain intersection cohomology groups.
The two bases for the Springer representation reminded Kazhdan and Lusztig of the two bases for the Grothendieck group
Grothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
of certain infinite dimensional representations of semisimple Lie algebras, given by Verma module
Verma module
Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
s and simple module
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
s. This analogy, and the work of Jantzen
Jens Carsten Jantzen
Jens Carsten Jantzen is a mathematician working on representation theory and algebraic groups, who introduced the Jantzen filtration, the Jantzen sum formula, the Jantzen conjecture, and translation functors.-References:**...
and Joseph relating primitive ideal
Primitive ideal
In mathematics, a left primitive ideal in ring theory is the annihilator of a simple left module. A right primitive ideal is defined similarly. Note that left and right primitive ideals are always two-sided ideals....
s of enveloping algebra
Enveloping algebra
Enveloping algebra in mathematics may refer to:* The universal enveloping algebra of a Lie algebra* The enveloping algebra of a general non-associative algebra...
s to representations of Weyl groups, led to the Kazhdan–Lusztig conjectures.
Definition
Fix a Coxeter group W with generating set S, and write ℓ(w) for the length of an element w (the smallest length of an expression for w as a product of elements of S). The Hecke algebraHecke algebra
In mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke and Nagayoshi Iwahori, is a one-parameter deformation of the group algebra of a Coxeter group....
of W has a basis of elements Tw for w∈W over the ring
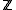 [q1/2, q−1/2], with multiplication defined by
[q1/2, q−1/2], with multiplication defined by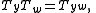 |
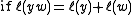 |
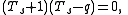 |
 |
The Kazhdan–Lusztig polynomials Pyw(q) are indexed by a pair of elements y, w of W, and uniquely determined by the following properties.
- They are 0 unless y ≤ w (in the Bruhat orderBruhat orderIn mathematics, the Bruhat order is a partial order on the elements of a Coxeter group, that corresponds to the inclusion order on Schubert varieties.-History:The Bruhat order on the Schubert varieties of a flag manifold or Grassmannian...
of W), 1 if y = w, and for y < w their degree is at most (ℓ(w) − ℓ(y) − 1)/2. - The elements
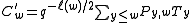
are invariant under the involution D of the Hecke algebra taking
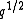 to
to  .
.and
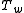 to
to 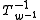 for all elements w ∈ W. The elements
for all elements w ∈ W. The elements 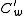 form a basis of the Hecke algebra as a
form a basis of the Hecke algebra as a  [q1/2, q−1/2]-module, called the Kazhdan–Lusztig basis.
[q1/2, q−1/2]-module, called the Kazhdan–Lusztig basis.To establish existence of the Kazhdan–Lusztig polynomials, Kazhdan and Lusztig gave a simple recursive procedure for computing the polynomials Pyw(q) in terms of more elementary polynomials denoted Ryw(q). defined by
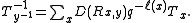
They can be computed using the recursion relations
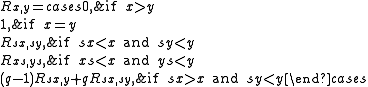
The Kazhdan–Lusztig polynomials can then be computed recursively using the relation

using the fact that the two terms on the left are polynomials in q1/2 and q−1/2 without constant term
Constant term
In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
s.
These formulas are tiresome to use by hand for rank greater than about 3, but are well adapted for computers, and the only limit on computing Kazhdan–Lusztig polynomials with them is that for large rank the number of such polynomials exceeds the storage capacity of computers.
Examples
- If y ≤ w then Py,w has constant term 1.
- If y ≤ w and l(w) − l(y) is 0, 1, or 2 then Py,w = 1.
- If w = w0 is the longest element of a finite Coxeter groupLongest element of a Coxeter groupIn mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating set consisting of simple reflections. It is often denoted by w0...
then Py,w = 1 for all y. - If W is the Coxeter group A1 or A2 (or more generally any Coxeter group of rank at most 2) then Py,w is 1 if y≤w and 0 otherwise.
- If W is the Coxeter group A3 with generating set S = {a, b, c} with a and c commuting then Pb,bacb = 1 + q and Pac,acbca = 1 + q, giving examples of non-constant polynomials.
- The simple values of Kazhdan–Lusztig polynomials for low rank groups are not typical of higher rank groups. For example, for the split form of E8 the most complicated Lusztig–Vogan polynomial (a variation of Kazhdan–Lusztig polynomials: see below) is
-
-
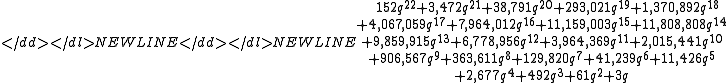
showed that any polynomial with constant term 1 and non-negative integer coefficients is the Kazhdan-Lusztig polynomial for some pair of elements of some symmetric group.
Kazhdan–Lusztig conjectures
The Kazhdan–Lusztig polynomials arise as transition coefficients between their canonical basis and the natural basis of the Hecke algebra. The Inventiones paper also put forth two equivalent conjectures, known now as Kazhdan–Lusztig conjectures, which related the values of their polynomials at 1 with representations of complex semisimple Lie groups and Lie algebras, addressing a long-standing problem in representation theory.
Let W be a finite Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
. For each w ∈ W denote by Mw be the Verma moduleVerma moduleVerma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
of highest weight −w(ρ)−ρ where ρ is the half-sum of positive roots (or Weyl vector), and let Lw be its irreducible quotient, the simple highest weight module of highest weight −w(ρ) − ρ. Both Mw and Lw are locally-finite weight modules over the complex semisimple Lie algebra g with the Weyl group W, and therefore admit an algebraic character. Let us write ch(X) for the character of a g-module X.
The Kazhdan-Lusztig conjectures state:
where w0 is the element of maximal length of the Weyl group.
These conjectures were proved independently by and by . The methods introduced in the course of the proof have guided development of representation theory throughout the 1980s and 1990s, under the name geometric representation theory.
Remarks
1. The two conjectures are known to be equivalent. Moreover, Borho–Jantzen's translation principle implies that ρ can be replaced by any dominant regular integral weight. Thus, Kazhdan-Lusztig conjectures describe the Jordan–Hölder multiplicities of Verma modules in any regular integral block of Bernstein–Gelfand–Gelfand category OCategory OCategory O is a mathematical object in representation theory of semisimple Lie algebras. It is a category whose objects arecertain representations of a semisimple Lie algebra and morphisms are homomorphisms of representations....
.
2. A similar interpretation of all coefficients of Kazhdan–Lusztig polynomials follows from the Jantzen conjecture, which roughly says that individual coefficients of Py,w are multiplicities of Ly in certain subquotient of the Verma module determined by a canonical filtration, the Jantzen filtration. The Jantzen conjecture in regular integral case was proved in a later paper of .
3. David VoganDavid VoganDavid Alexander Vogan is a mathematician at M.I.T. who works on unitary representations of simple Lie groups. He is one of the participants in the Atlas of Lie Groups and Representations.-Publications:*Some online by Vogan...
showed as a consequence of the conjectures that
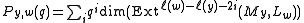
and that Extj(My,Lw) vanishes if j + ℓ(w) + ℓ(y) is odd, so the dimensions of all such Ext groups in category O are determined in terms of coefficients of Kazhdan–Lusztig polynomials. This result demonstrates that all coefficients of the Kazhdan–Lusztig polynomials of a finite Weyl group are non-negative integers. However, positivity for the case of a finite Weyl group W was already known from the interpretation of coefficients of the Kazhdan–Lusztig polynomials as the dimensions of intersection cohomology groups, irrespective of the conjectures. Conversely, the relation between Kazhdan–Lusztig polynomials and the Ext groups theoretically can be used to prove the conjectures, although this approach to proving them turned out to be more difficult to carry out.
4. Some special cases of the Kazhdan–Lusztig conjectures are easy to verify. For example, M1 is the antidominant Verma module, which is known to be simple. This means that M1 = L1, establishing the second conjecture for w = 1, since the sum reduces to a single term. On the other hand, the first conjecture for w = w0 follows from the Weyl character formulaWeyl character formulaIn mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
and the formula for the character of a Verma module, together with the fact that all Kazhdan-Lusztig polynomials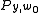 are equal to 1.
are equal to 1.
5. Kashiwara (1990) proved a generalization of the Kazhdan–Lusztig conjectures to symmetrizable Kac–Moody algebraKac–Moody algebraIn mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
s.
Relation to intersection cohomology of Schubert varieties
By the Bruhat decompositionBruhat decompositionIn mathematics, the Bruhat decomposition G = BWB into cells can be regarded as a general expression of the principle of Gauss–Jordan elimination, which generically writes a matrix as a product of an upper triangular and lower triangular matrices—but with exceptional cases...
the space G/B of the algebraic group G with Weyl group W is a disjoint union of affine spaces Xw parameterized by elements w of W.
The closures of these spaces Xw are called Schubert varieties, and Kazhdan and Lusztig, following a suggestion of Deligne, showed how to express Kazhdan-Lusztig polynomials in terms of intersection cohomology groups of Schubert varieties.
More precisely, the Kazhdan-Lusztig polynomial Py,w(q) is equal to
where each term on the right means: take the complex IC of sheaves whose hyperhomology is the intersection homology of the Schubert varietySchubert varietyIn algebraic geometry, a Schubert variety is a certain subvariety of a Grassmannian, usually with singular points. Described by means of linear algebra, a typical example consists of the k-dimensional subspaces V of an n dimensional vector space W, such that\dim\ge jfor j = 1, 2, ..., k,...
of w (the closure of the cell Xw), take its cohomology of degree 2i, and then take the dimension of the stalk of this sheaf at any point of the cell Xy whose closure is the Schubert variety of y. The odd dimensional cohomology groups do not appear in the sum because they are all zero.
This gave the first proof that all coefficients of Kazhdan–Lusztig polynomials for finite Weyl groups are non-negative integers.
Generalization to real groups
Lusztig–Vogan polynomials (also called Kazhdan–Lusztig polynomials or Kazhdan–Lusztig–Vogan polynomials) were introduced in . They are analogous to Kazhdan-Lusztig polynomials, but are tailored to representations of real semisimple Lie groups, and play major role in the conjectural description of their unitary duals. Their definition is more complicated, reflecting relative complexity of representations of real groups compared to complex groups.
The distinction, in the cases directly connection to representation theory, is explained on the level of double cosetDouble cosetIn mathematics, an double coset in G, where G is a group and H and K are subgroups of G, is an equivalence class for the equivalence relation defined on G by...
s; or in other terms of actions on analogues of complex flag manifoldFlag manifoldIn mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
s G/B where G is a complex Lie group and B a Borel subgroupBorel subgroupIn the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
. The original (K-L) case is then about the details of decomposing
- B\G/B,
a classical theme of the Bruhat decompositionBruhat decompositionIn mathematics, the Bruhat decomposition G = BWB into cells can be regarded as a general expression of the principle of Gauss–Jordan elimination, which generically writes a matrix as a product of an upper triangular and lower triangular matrices—but with exceptional cases...
, and before that of Schubert cells in a GrassmannianGrassmannianIn mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
. The L-V case takes a real form GR of G, a maximal compact subgroupMaximal compact subgroupIn mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
KR in that semisimple group GR, and makes the complexificationComplexificationIn mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
K of KR. Then the relevant object of study is
- K\G/B.
In March 2007, it was announced that the L-V polynomials had been calculated for the split form of E8.
Generalization to other objects in representation theory
The second paper of Kazhdan and Lusztig established a geometric setting for definition of Kazhdan–Lusztig polynomials, namely, the geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
of singularities of Schubert varieties in the flag variety. Much of the later work of Lusztig explored analogues of Kazhdan–Lusztig polynomials in the context of other natural singular algebraic varieties arising in representation theory, in particular, closures of nilpotent orbitNilpotent orbitNilpotent orbits are generalizations of nilpotent matrices that play an important rolein representation theory of real and complex semisimple Lie groups and semisimple Lie algebras.- Definition :...
s and quiver varieties. It turned out that the representation theory of quantum groups, modular Lie algebraModular Lie algebraIn mathematics, a modular Lie algebra is a Lie algebra over a field of positive characteristic.The theory of modular Lie algebras is significantly different from the theory of real and complex Lie algebras...
s and affine Hecke algebraAffine Hecke algebraIn mathematics, an affine Hecke algebra is the Hecke algebra of an affine Weyl group, and can be used to prove Macdonald's constant term conjecture for Macdonald polynomials.-Definition:...
s are all tightly controlled by appropriate analogues of Kazhdan–Lusztig polynomials. They admit an elementary description, but the deeper properties of these polynomials necessary for representation theory follow from sophisticated techniques of modern algebraic geometry and homological algebraHomological algebraHomological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, such as the use of intersection cohomologyIntersection cohomologyIn topology, a branch of mathematics, intersection homology is an analogue of singular homology especially well-suited for the study of singular spaces, discovered by Mark Goresky and Robert MacPherson in the fall of 1974 and developed by them over the next few years.Intersection cohomology was...
, perverse sheaves and Beilinson–Bernstein–Deligne decomposition.
The coefficients of the Kazhdan–Lusztig polynomials are conjectured to be the dimensions of some homomorphism spaces in Soergel's bimodule category. This is the only known positive interpretation of these coefficients for arbitrary Coxeter groups.
Combinatorial theory
Combinatorial properties of Kazhdan–Lusztig polynomials and their generalizations are a topic of active current research. Given their significance in representation theory and algebraic geometry, attempts have been undertaken to develop the theory of Kazhdan–Lusztig polynomials in purely combinatorial fashion, relying to some extent on geometry, but without reference to intersection cohomology and other advanced techniques. This has led to exciting developments in algebraic combinatoricsAlgebraic combinatoricsAlgebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra....
, such as pattern-avoidance phenomenon. Some references are given in the textbook of . A research monograph on the subject is .
, there is no known combinatorial interpretation of all the coefficients of the Kazhdan–Lusztig polynomials (as the cardinalities of some natural sets) even for the symmetric groups, though explicit formulas exist in many special cases.
External links
-
-