
Schubert variety
Encyclopedia
In algebraic geometry
, a Schubert variety is a certain subvariety
of a Grassmannian
, usually with singular points
. Described by means of linear algebra
, a typical example consists of the k-dimensional subspaces V of an n dimensional vector space W, such that

for j = 1, 2, ..., k, where
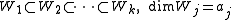
is a certain flag of subspaces in W and 0 < a1 < ... < ak ≤ n. More generally, given a semisimple
algebraic group
G with a Borel subgroup
B and a standard parabolic subgroup P, it is known that the homogeneous space
X = G/P, which is an example of a flag variety, consists of finitely many B-orbits that may be parametrized by certain elements of the Weyl group
W. The closure of the B-orbit associated to an element w of the Weyl group is denoted by Xw and is called a Schubert variety in G/P. The classical case corresponds to G = SLn and P being the kth maximal parabolic subgroup of G.
s, which encode their local Goresky–MacPherson intersection cohomology
.
The algebras of regular functions on Schubert varieties have deep significance in algebraic combinatorics
and are examples of algebras with a straightening law. (Co)homology of the Grassmanian, and more generally, of more general flag varieties, is spanned by the (co)homology classes of Schubert varieties, the Schubert cycles. The study of the intersection theory on the Grassmanian was initiated by Hermann Schubert
and continued by Zeuthen
in 19th century under the heading of enumerative geometry
. This area was deemed by David Hilbert
important enough to be included as the fifteenth
of his celebrated 23 problems. The study continued in 20th century as part of the general development of algebraic topology
and representation theory
, but accelerated in the 1990s beginning with the work of William Fulton on the degeneracy loci and Schubert polynomial
s, following up on earlier investigations of Bernstein
–Gelfand
–Gelfand and Demazure in representation theory in the 1970s, Lascoux
and Schützenberger
in combinatorics in the 1980s and of Fulton and MacPherson in intersection theory
of singular algebraic varieties, also in the 1980s.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a Schubert variety is a certain subvariety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
of a Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
, usually with singular points
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
. Described by means of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a typical example consists of the k-dimensional subspaces V of an n dimensional vector space W, such that

for j = 1, 2, ..., k, where
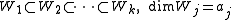
is a certain flag of subspaces in W and 0 < a1 < ... < ak ≤ n. More generally, given a semisimple
Semisimple algebraic group
In mathematics, especially in the areas of abstract algebra and algebraic geometry studying linear algebraic groups, a semisimple algebraic group is a type of matrix group which behaves much like a semisimple Lie algebra or semisimple ring.- Definition :...
algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
G with a Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
B and a standard parabolic subgroup P, it is known that the homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
X = G/P, which is an example of a flag variety, consists of finitely many B-orbits that may be parametrized by certain elements of the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
W. The closure of the B-orbit associated to an element w of the Weyl group is denoted by Xw and is called a Schubert variety in G/P. The classical case corresponds to G = SLn and P being the kth maximal parabolic subgroup of G.
Significance
Schubert varieties form one of the most important and best studied classes of singular algebraic varieties. A certain measure of singularity of Schubert varieties is provided by Kazhdan–Lusztig polynomialKazhdan–Lusztig polynomial
In representation theory, a Kazhdan–Lusztig polynomial Py,w is a member of a family of integral polynomials introduced by . They are indexed by pairs of elements y, w of a Coxeter group W, which can in particular be the Weyl group of a Lie group.- Motivation and history:In the spring of 1978...
s, which encode their local Goresky–MacPherson intersection cohomology
Intersection cohomology
In topology, a branch of mathematics, intersection homology is an analogue of singular homology especially well-suited for the study of singular spaces, discovered by Mark Goresky and Robert MacPherson in the fall of 1974 and developed by them over the next few years.Intersection cohomology was...
.
The algebras of regular functions on Schubert varieties have deep significance in algebraic combinatorics
Algebraic combinatorics
Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra....
and are examples of algebras with a straightening law. (Co)homology of the Grassmanian, and more generally, of more general flag varieties, is spanned by the (co)homology classes of Schubert varieties, the Schubert cycles. The study of the intersection theory on the Grassmanian was initiated by Hermann Schubert
Hermann Schubert
Hermann Cäsar Hannibal Schubert was a German mathematician.Schubert was one of the leading developers of enumerative geometry, which considers those parts of algebraic geometry that involve a finite number of solutions. In 1874, Schubert won a prize for solving a question posed by Zeuthen...
and continued by Zeuthen
Hieronymus Georg Zeuthen
Hieronymus Georg Zeuthen was a Danish mathematician.He is known for work on the enumerative geometry of conic sections, algebraic surfaces, and history of mathematics.-Biography:...
in 19th century under the heading of enumerative geometry
Enumerative geometry
In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory.-History:...
. This area was deemed by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
important enough to be included as the fifteenth
Hilbert's fifteenth problem
Hilbert's fifteenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert. It entails a rigorous foundation of Schubert's enumerative calculus....
of his celebrated 23 problems. The study continued in 20th century as part of the general development of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, but accelerated in the 1990s beginning with the work of William Fulton on the degeneracy loci and Schubert polynomial
Schubert polynomial
In mathematics, Schubert polynomials are generalizations of Schur polynomials that represent cohomology classes of Schubert cycles in flag varieties.They were introduced by and are named after Hermann Schubert.-Background:...
s, following up on earlier investigations of Bernstein
Joseph Bernstein
Joseph Bernstein is an Israeli mathematician working at Tel Aviv University. He works in algebraic geometry, representation theory, and number theory....
–Gelfand
Israel Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
–Gelfand and Demazure in representation theory in the 1970s, Lascoux
Alain Lascoux
Alain Lascoux is a French mathematician at the University of Marne la Vallée and Nankai University. His research fields include algebraic combinatorics, particuarly Hecke algebra and Young tableau....
and Schützenberger
Marcel-Paul Schützenberger
Marcel-Paul "Marco" Schützenberger was a French mathematician and Doctor of Medicine. His work had impact across the fields of formal language, combinatorics, and information theory...
in combinatorics in the 1980s and of Fulton and MacPherson in intersection theory
Intersection theory
In mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
of singular algebraic varieties, also in the 1980s.

