
Category O
Encyclopedia
Category O is a mathematical
object in representation theory
of semisimple Lie algebras. It is a category
whose objects are
certain representations of a semisimple Lie algebra and morphisms are homomorphisms of representations.
 is a (usually complex) semisimple Lie algebra with a Cartan subalgebra
is a (usually complex) semisimple Lie algebra with a Cartan subalgebra
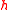 ,
,  is a root system
is a root system
and is a system of positive roots. Denote by
is a system of positive roots. Denote by 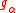
the root space corresponding to a root and
and 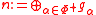 a nilpotent subalgebra.
a nilpotent subalgebra.
If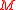 is a
is a 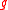 -module and
-module and 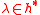 , then
, then 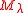 is the weight space
is the weight space
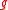 -modules
-modules 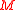 such that
such that
Morphisms of this category are the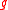 -homomorphisms of these modules.
-homomorphisms of these modules.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
object in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of semisimple Lie algebras. It is a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
whose objects are
certain representations of a semisimple Lie algebra and morphisms are homomorphisms of representations.
Introduction
Assume that is a (usually complex) semisimple Lie algebra with a Cartan subalgebra
is a (usually complex) semisimple Lie algebra with a Cartan subalgebra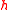 ,
,  is a root system
is a root systemRoot system of a semi-simple Lie algebra
In mathematics, there is a one-to-one correspondence between reduced crystallographic root systems and semi-simple Lie algebras. We show the construction of a root system from a semi-simple Lie algebra and conversely, the construction of a semi-simple Lie algebra from a reduced crystallographic...
and
 is a system of positive roots. Denote by
is a system of positive roots. Denote by 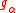
the root space corresponding to a root
 and
and 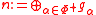 a nilpotent subalgebra.
a nilpotent subalgebra.If
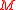 is a
is a 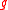 -module and
-module and 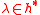 , then
, then 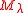 is the weight space
is the weight space
Definition of category O
The objects of category O are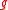 -modules
-modules 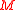 such that
such that
-
 is finitely generated
is finitely generated -
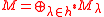
-
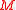 is locally
is locally  -finite, i.e. for each
-finite, i.e. for each  , the
, the  -module generated by
-module generated by  is finite-dimensional.
is finite-dimensional.
Morphisms of this category are the
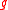 -homomorphisms of these modules.
-homomorphisms of these modules.Basic properties
- Each module in a category O has finite-dimensional weight spaces.
- Each module in category O is a Noetherian moduleNoetherian moduleIn abstract algebra, an Noetherian module is a module that satisfies the ascending chain condition on its submodules, where the submodules are partially ordered by inclusion....
. - O is an abelian categoryAbelian categoryIn mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
- O is closed to submodules, quotients and finite direct sums
- Objects in O are
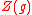 -finite, i.e. if
-finite, i.e. if 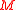 is an object and
is an object and 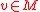 , then the subspace
, then the subspace  generated by
generated by  under the action of the centerCenter (algebra)The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
under the action of the centerCenter (algebra)The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
of the universal enveloping algebraUniversal enveloping algebraIn mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
, is finite-dimensional.
Examples
- All finite-dimensional
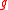 -modules and their
-modules and their 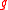 -homomorphisms are in category O.
-homomorphisms are in category O. - Verma moduleVerma moduleVerma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
s and generalized Verma moduleGeneralized Verma moduleIn mathematics, generalized Verma modules are a generalization of a Verma module, and are objects in the representation theory of Lie algebras. They were studied originally by James Lepowsky in the nineteen seventies. The motivation for their study is that their homomorphisms correspond to...
s and their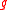 -homomorphisms) are in category O.
-homomorphisms) are in category O.
See also
- Highest-weight module
- Universal enveloping algebraUniversal enveloping algebraIn mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
- Highest-weight category

