Nilpotent orbit
Encyclopedia
Nilpotent orbits are generalizations of nilpotent
matrices
that play an important role
in representation theory
of real and complex semisimple Lie groups and semisimple Lie algebras.
is nilpotent, that is, (ad X)n = 0 for large enough n. Equivalently, X is nilpotent if its characteristic polynomial
pad X(t) is equal to tdim g.
A semisimple Lie group
or algebraic group
G acts on its Lie algebra via the adjoint representation
, and the property of being nilpotent is invariant under this action. A nilpotent orbit is an orbit of the adjoint action such that any (equivalently, all) of its elements is (are) nilpotent.
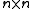matrices with complex entries form the main motivating case for the general theory, corresponding to the complex general linear group
. From the Jordan normal form
of matrices we know that each nilpotent matrix is conjugate to a unique matrix with Jordan blocks of sizes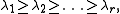
where 
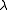is a partition
of n. Thus in the case n=2 there are two nilpotent orbits, the zero orbit consisting of the zero matrix and corresponding to the partition (1,1) and the principal orbit consisting of all non-zero matrices A with zero trace and determinant,
corresponding to the partition (2). Geometrically, this orbit is a two-dimensional complex quadratic cone
in four dimensional vector space of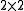
matrices minus its apex.
The complex special linear group
is a subgroup of the general linear group with the same nilpotent orbits. However, if we replace the complex special linear group with the real special linear group, new nilpotent orbits may arise. In particular, for n=2 there are now 3 nilpotent orbits: the zero orbit and two real half-cones (without the apex), corresponding to positive and negative values of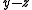
in the parametrization above.
: given two nilpotent orbits, O1 is less than or equal to O2 if O1 is contained in the Zariski closure of O2. This poset has a unique minimal element, zero orbit, and unique
maximal element, the regular nilpotent orbit, but in general, it is not a graded poset
.
If the ground field is algebraically closed then the zero orbit is covered
by a unique orbit, called the minimal orbit, and the regular orbit covers a unique orbit, called the subregular orbit.
In the case of the special linear group
SLn, the nilpotent orbits are parametrized by the partitions
of n. By a theorem of Gerstenhaber
, the ordering of the orbits corresponds to the dominance order
on the partitions of n. Moreover, if G is an isometry group of a bilinear form
, i.e. an orthogonal or symplectic subgroup of SLn, then its nilpotent orbits are parametrized by partitions of n satisfying a certain parity condition and the corresponding poset structure is induced by the dominance order on all partitions (this is a nontrivial theorem, due to Gerstenhaber and Hesselink).
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that play an important role
in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of real and complex semisimple Lie groups and semisimple Lie algebras.
Definition
An element X of a semisimple Lie algebra g is called nilpotent if its adjoint endomorphismAdjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
- ad X: g → g, ad X(Y) = [X,Y]
is nilpotent, that is, (ad X)n = 0 for large enough n. Equivalently, X is nilpotent if its characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
pad X(t) is equal to tdim g.
A semisimple Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
or algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
G acts on its Lie algebra via the adjoint representation
Adjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
, and the property of being nilpotent is invariant under this action. A nilpotent orbit is an orbit of the adjoint action such that any (equivalently, all) of its elements is (are) nilpotent.
Examples
Nilpotent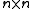 matrices with complex entries form the main motivating case for the general theory, corresponding to the complex general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
. From the Jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
of matrices we know that each nilpotent matrix is conjugate to a unique matrix with Jordan blocks of sizes
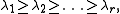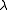where is a partitionPartition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of n. Thus in the case n=2 there are two nilpotent orbits, the zero orbit consisting of the zero matrix and corresponding to the partition (1,1) and the principal orbit consisting of all non-zero matrices A with zero trace and determinant,
-
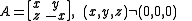with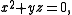 
corresponding to the partition (2). Geometrically, this orbit is a two-dimensional complex quadratic cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
in four dimensional vector space of
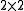matrices minus its apex.The complex special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
is a subgroup of the general linear group with the same nilpotent orbits. However, if we replace the complex special linear group with the real special linear group, new nilpotent orbits may arise. In particular, for n=2 there are now 3 nilpotent orbits: the zero orbit and two real half-cones (without the apex), corresponding to positive and negative values of
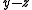in the parametrization above.Properties
- Nilpotent orbits can be characterized as those orbits of the adjoint action whose Zariski closure contains 0.
- Nilpotent orbits are finite in number.
- The Zariski closure of a nilpotent orbit is a union of nilpotent orbits.
- Jacobson–Morozov theorem: over a field of characteristic zero, any nilpotent element e can be included into an sl2-tripleSl2-tripleIn the theory of Lie algebras, an sl2-triple is a triple of elements of a Lie algebra that satisfy the commutation relations between the standard generators of the special linear Lie algebra sl2...
{e,h,f} and all such triples are conjugate by ZG(e), the centralizer of e in G. Together with the representation theory of sl2, this allows one to label nilpotent orbits by finite combinatorial data, giving rise to the Dynkin–Kostant classification of nilpotent orbits.
Poset structure
Nilpotent orbits form a partially ordered setPartially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
: given two nilpotent orbits, O1 is less than or equal to O2 if O1 is contained in the Zariski closure of O2. This poset has a unique minimal element, zero orbit, and unique
maximal element, the regular nilpotent orbit, but in general, it is not a graded poset
Graded poset
In mathematics, in the branch of combinatorics, a graded poset, sometimes called a ranked poset , is a partially ordered set P equipped with a rank function ρ from P to N compatible with the ordering such that whenever y covers x, then...
.
If the ground field is algebraically closed then the zero orbit is covered
Covering relation
In mathematics, especially order theory, the covering relation of a partially ordered set is the binary relation which holds between comparable elements that are immediate neighbours...
by a unique orbit, called the minimal orbit, and the regular orbit covers a unique orbit, called the subregular orbit.
In the case of the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SLn, the nilpotent orbits are parametrized by the partitions
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of n. By a theorem of Gerstenhaber
Murray Gerstenhaber
Murray Gerstenhaber is an American mathematician, professor of mathematics at the University of Pennsylvania, best known for his contributions to theoretical physics with his discovery of Gerstenhaber algebra.- About :...
, the ordering of the orbits corresponds to the dominance order
Dominance order
Dominance order is a partial order on the set of partitions of a positive integer n that plays an important role in algebraic combinatorics and representation theory, especially in the context of symmetric functions and representation theory of the symmetric group.- Definition :If...
on the partitions of n. Moreover, if G is an isometry group of a bilinear form
Classical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
, i.e. an orthogonal or symplectic subgroup of SLn, then its nilpotent orbits are parametrized by partitions of n satisfying a certain parity condition and the corresponding poset structure is induced by the dominance order on all partitions (this is a nontrivial theorem, due to Gerstenhaber and Hesselink).