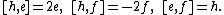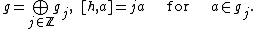In the theory of Lie algebra

Lie algebra

In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

s, an sl₂-triple is a triple of elements of a Lie algebra that satisfy the commutation relations between the standard generators of the special linear

Special linear group

In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....

 Lie algebra sl₂. This notion plays an important role in the theory of semisimple Lie algebras, especially in regards to their nilpotent orbit

Nilpotent orbit

Nilpotent orbits are generalizations of nilpotent matrices that play an important rolein representation theory of real and complex semisimple Lie groups and semisimple Lie algebras.- Definition :...

s.

Definition

Elements {e,h,f} of a Lie algebra g form an sl₂-triple if

These commutation relations are satisfied by the generators

of the Lie algebra sl₂ of 2 by 2 matrices with zero trace

Trace (linear algebra)

In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...

. It follows that sl₂-triples in g are in a bijective correspondence with the Lie algebra homomorphism

Homomorphism

In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...

s from sl₂ into g.

The alternative notation for the elements of an sl₂-triple is {H, X, Y}, with H corresponding to h, X corresponding to e, and Y corresponding to f.

Properties

Assume that g is a Lie algebra over a field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

 of characteristic zero.
From the representation theory of the Lie algebra sl₂, one concludes that the Lie algebra g decomposes into a direct sum of finite-dimensional subspaces, each of which is isomorphic to V_j, the j + 1-dimensional simple sl₂-module with highest weight j. The element h of the sl₂-triple is semisimple, with the simple eigenvalues j, j − 2, …, −j on a submodule of g isomorphic to V_j . The elements e and f move between different eigenspaces of h, increasing the eigenvalue by 2 in case of e and decreasing it by 2 in case of f. In particular, e and f are nilpotent elements

Nilpotent orbit

Nilpotent orbits are generalizations of nilpotent matrices that play an important rolein representation theory of real and complex semisimple Lie groups and semisimple Lie algebras.- Definition :...

 of the Lie algebra g.
Conversely, the Jacobson–Morozov theorem states that any nilpotent element e of a semisimple Lie algebra g can be included into an sl₂-triple {e,h,f}, and all such triples are conjugate under the action of the group Z_G(e), the centralizer of e in the adjoint Lie group G corresponding to the Lie algebra g.
The semisimple element h of any sl₂-triple containing a given nilpotent element e of g is called a characteristic of e.

An sl₂-triple defines a grading on g according to the eigenvalues of h:

The sl₂-triple is called even if only even j occur in this decomposition, and odd otherwise.

If g is a semisimple Lie algebra, then g₀ is a reductive Lie subalgebra of g (it is not semisimple in general). Moreover, the direct sum of the eigenspaces of h with non-negative eigenvalues is a parabolic subalgebra of g with the Levi component g0.

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.