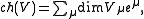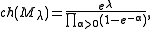Algebraic character
Encyclopedia
Algebraic character is a formal expression attached to a module in representation theory
of semisimple Lie algebras that generalizes the character of a finite-dimensional representation
and is analogous to the Harish-Chandra character
of the representations of semisimple Lie groups.
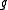be a semisimple Lie algebra with a fixed Cartan subalgebra 
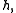and let the abelian group 
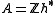consist of the (possibly infinite) formal integral linear combinations of 
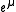, where 
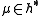, the (complex) vector space of weights. Suppose that 
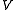is a locally-finite weight module. Then the algebraic character of 
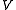is an element of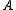 
defined by the formula:
where the sum is taken over all weight spaces of the module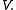
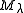with the highest weight 
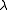is given by the formula
with the product taken over the set of positive roots.
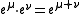and extend it to their finite linear combinations by linearity, this does not make 
into a ring, because of the possibility of formal infinite sums. Thus the product of algebraic characters is well defined only in restricted situations; for example, for the case of a highest weight module, or a finite-dimensional module. In good situations, the algebraic character is multiplicative, i.e., the character of the tensor product of two weight modules is the product of their characters.
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of semisimple Lie algebras that generalizes the character of a finite-dimensional representation
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
and is analogous to the Harish-Chandra character
Harish-Chandra character
In mathematics, the Harish-Chandra character, named after Harish-Chandra, of a representation of a semisimple Lie group G on a Hilbert space H is a distribution on the group G that is analogous to the character of a finite dimensional representation of a compact group.-Definition:Suppose that π...
of the representations of semisimple Lie groups.
Definition
Let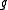 be a semisimple Lie algebra with a fixed Cartan subalgebra 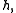and let the abelian group 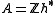consist of the (possibly infinite) formal integral linear combinations of 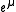, where 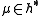, the (complex) vector space of weights. Suppose that 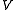is a locally-finite weight module. Then the algebraic character of 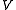is an element of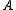 defined by the formula:
where the sum is taken over all weight spaces of the module
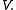
Example
The algebraic character of the Verma moduleVerma module
Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
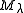with the highest weight 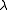is given by the formula
with the product taken over the set of positive roots.
Properties
Algebraic characters are defined for locally-finite weight modules and are additive, i.e. the character of a direct sum of modules is the sum of their characters. On the other hand, although one can define multiplication of the formal exponents by the formula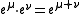 and extend it to their finite linear combinations by linearity, this does not make into a ring, because of the possibility of formal infinite sums. Thus the product of algebraic characters is well defined only in restricted situations; for example, for the case of a highest weight module, or a finite-dimensional module. In good situations, the algebraic character is multiplicative, i.e., the character of the tensor product of two weight modules is the product of their characters.