Interaction picture
Encyclopedia
In quantum mechanics
, the Interaction picture (or Dirac picture) is an intermediate between the Schrödinger picture
and the Heisenberg picture
. Whereas in the other two pictures either the state vector
or the operators
carry time dependence, in the interaction picture both carry part of the time dependence of observable
s.
Equations that include operators acting at different times, which hold in the interaction picture, don't necessarily hold in the Schrödinger or the Heisenberg picture. This is because time-dependent unitary transformations relate operators in one picture to the analogous operators in the others. Not all textbooks and articles make explicit which picture each operator comes from, which can lead to confusion and mistakes.
) to those same operators and state vectors in the Schrödinger picture.
To switch into the interaction picture, we divide the Schrödinger picture Hamiltonian
into two parts,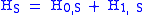
. (Any possible choice of parts will yield a valid interaction picture; but in order for the interaction picture to be useful in simplifying the analysis of a problem, the parts will typically be chosen so that 
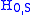is well understood and exactly solvable, and 
contains some harder-to-analyze perturbation to this system.)
If the Hamiltonian has explicit time-dependence (for example, if the quantum system interacts with an applied external electric field that varies in time), it will usually be advantageous to include the explicitly time-dependent terms with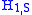
, leaving 
time-independent. We will proceed assuming that this is the case. (If there is a context in which it makes sense to have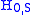 
be time-dependent, then one can proceed by replacing 
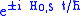by the corresponding time-evolution operator
in the definitions below.)
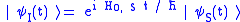
(where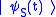
is the same state vector in the Schrödinger picture.)
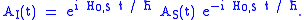
(Note that the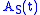
will typically not depend on t, and can be rewritten as just 
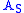. It only depends on t if the operator has "explicit time dependence", for example due to its dependence on an applied, external, time-varying electric field.)
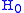itself, the interaction picture and Schrödinger picture are the same:
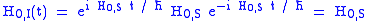
(this can be proved using the fact that operators commute
with differentiable functions of themselves.) This particular operator can thus be called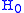
with no ambiguity.
For the perturbation Hamiltonian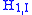
, we have:
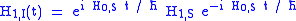
where the interaction picture perturbation Hamiltonian becomes a time-dependent Hamiltonian (unless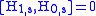
).
It is possible to obtain the interaction picture for a time-dependent Hamiltonian
as well but the exponentials need to be replaced by the unitary propagator for the evolution due to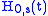 
or more explicitly with a time-ordered exponential integral.
can be shown to transform to the interaction picture in the same way as any other operator. In particular, let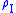
and 
be the density matrix in the interaction picture and the Schrödinger picture, respectively. If there is probability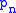 
to be in the physical state 
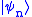, then
into the interaction picture gives:
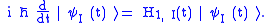
This equation is referred to as the Schwinger
-Tomonaga
equation.
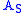is time independent (i.e., does not have "explicit time dependence"; see above), then the corresponding time evolution for 
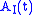is given by:
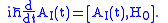
In the interaction picture the operators evolve in time like the operators in the Heisenberg picture
with
the Hamiltonian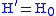
.
(or equivalently, transforming the von Neumann equation into the interaction picture) gives:
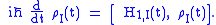
The interaction picture is convenient when considering the effect of a small interaction term, H1, S, being added to the Hamiltonian of a solved system, H0, S. By switching into the interaction picture, you can use time-dependent perturbation theory to find the effect of H1, I.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the Interaction picture (or Dirac picture) is an intermediate between the Schrödinger picture
Schrödinger picture
In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...
and the Heisenberg picture
Heisenberg picture
In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
. Whereas in the other two pictures either the state vector
State vector
*A state vector in general control systems describes the observed states of an object in state space, e.g. in variables of the degrees of freedom for motion *A state vector in general control systems describes the observed states of an object in state space, e.g. in variables of the degrees of...
or the operators
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
carry time dependence, in the interaction picture both carry part of the time dependence of observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
s.
Equations that include operators acting at different times, which hold in the interaction picture, don't necessarily hold in the Schrödinger or the Heisenberg picture. This is because time-dependent unitary transformations relate operators in one picture to the analogous operators in the others. Not all textbooks and articles make explicit which picture each operator comes from, which can lead to confusion and mistakes.
Definition
Operators and state vectors in the interaction picture are related by a change of basis (unitary transformationUnitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
) to those same operators and state vectors in the Schrödinger picture.
To switch into the interaction picture, we divide the Schrödinger picture Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
into two parts,
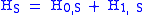. (Any possible choice of parts will yield a valid interaction picture; but in order for the interaction picture to be useful in simplifying the analysis of a problem, the parts will typically be chosen so that 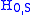is well understood and exactly solvable, and contains some harder-to-analyze perturbation to this system.)If the Hamiltonian has explicit time-dependence (for example, if the quantum system interacts with an applied external electric field that varies in time), it will usually be advantageous to include the explicitly time-dependent terms with
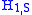, leaving time-independent. We will proceed assuming that this is the case. (If there is a context in which it makes sense to have 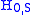be time-dependent, then one can proceed by replacing 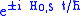by the corresponding time-evolution operatorSchrödinger picture
In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...
in the definitions below.)
State vectors
A state vector in the interaction picture is defined as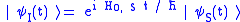(where
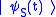is the same state vector in the Schrödinger picture.)Operators
An operator in the interaction picture is defined as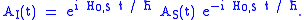(Note that the
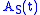will typically not depend on t, and can be rewritten as just 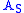. It only depends on t if the operator has "explicit time dependence", for example due to its dependence on an applied, external, time-varying electric field.)Hamiltonian operator
For the operator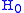 itself, the interaction picture and Schrödinger picture are the same: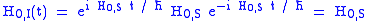(this can be proved using the fact that operators commute
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
with differentiable functions of themselves.) This particular operator can thus be called
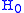with no ambiguity.For the perturbation Hamiltonian
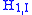, we have: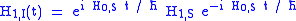where the interaction picture perturbation Hamiltonian becomes a time-dependent Hamiltonian (unless
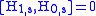).It is possible to obtain the interaction picture for a time-dependent Hamiltonian
as well but the exponentials need to be replaced by the unitary propagator for the evolution due to 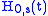or more explicitly with a time-ordered exponential integral.Density matrix
The density matrixDensity matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
can be shown to transform to the interaction picture in the same way as any other operator. In particular, let
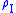and be the density matrix in the interaction picture and the Schrödinger picture, respectively. If there is probability 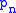to be in the physical state 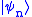, thenTime-evolution of states
Transforming the Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
into the interaction picture gives:
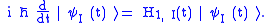
This equation is referred to as the Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
-Tomonaga
Sin-Itiro Tomonaga
was a Japanese physicist, influential in the development of quantum electrodynamics, work for which he was jointly awarded the Nobel Prize in Physics in 1965 along with Richard Feynman and Julian Schwinger.-Biography:...
equation.
Time-evolution of operators
If the operator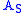 is time independent (i.e., does not have "explicit time dependence"; see above), then the corresponding time evolution for 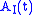is given by: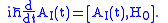In the interaction picture the operators evolve in time like the operators in the Heisenberg picture
Heisenberg picture
In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
with
the Hamiltonian
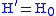.Time-evolution of the density matrix
Transforming the Schwinger-Tomonaga equation into the language of the density matrixDensity matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
(or equivalently, transforming the von Neumann equation into the interaction picture) gives:
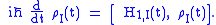
Use of interaction picture
The purpose of the interaction picture is to shunt all the time dependence due to H0 onto the operators, leaving only H1, I affecting the time-dependence of the state vectors.The interaction picture is convenient when considering the effect of a small interaction term, H1, S, being added to the Hamiltonian of a solved system, H0, S. By switching into the interaction picture, you can use time-dependent perturbation theory to find the effect of H1, I.