Kramers-Kronig relation
Encyclopedia
The Kramers–Kronig relations are bidirectional mathematical
relations, connecting the real
and imaginary
parts of any complex function
that is analytic
in the upper half-plane. These relations are often used to calculate the real part from the imaginary part (or vice versa) of response functions
in physical system
s because causality
implies the analyticity condition is satisfied, and conversely, analyticity implies causality of the corresponding physical system. The relation is named in honor of Ralph Kronig
and Hendrik Anthony Kramers
.
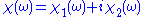 be a complex function of the complex variable
be a complex function of the complex variable  , where
, where 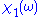 and
and 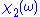 are real
are real
. Suppose this function is analytic
in the upper half-plane of and it vanishes faster than
and it vanishes faster than 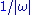 as
as  . The Kramers–Kronig relations are given by
. The Kramers–Kronig relations are given by
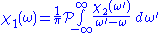
and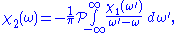
where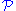 denotes the Cauchy principal value
denotes the Cauchy principal value
. We see that the real and imaginary parts of such a function are not independent, so that the full function can be reconstructed given just one of its parts.
for complex integration. Given any analytic function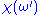 in the upper half plane, the function
in the upper half plane, the function 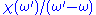 where
where  is real will also be analytic in the upper half of the plane. The residue theorem consequently states that
is real will also be analytic in the upper half of the plane. The residue theorem consequently states that
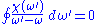
 for any contour
for any contour
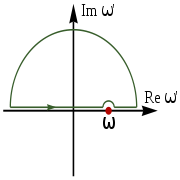
within this region. We choose the contour to trace the real axis, a hump over the pole at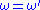 , and a semicircle in the upper half plane at infinity. We then decompose the integral into its contributions along each of these three contour segments. The length of the segment at infinity increases proportionally to
, and a semicircle in the upper half plane at infinity. We then decompose the integral into its contributions along each of these three contour segments. The length of the segment at infinity increases proportionally to  , but its integral component vanishes as long as
, but its integral component vanishes as long as 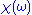 vanishes faster than
vanishes faster than 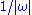 . We are left with the segment along the real axis and the half-circle around the pole:
. We are left with the segment along the real axis and the half-circle around the pole:
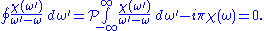
The second term in the middle expression is obtained using the theory of residues. Rearranging, we arrive at the compact form of the Kramers–Kronig relations,
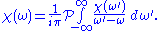
The single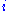 in the denominator hints at the connection between the real and imaginary components. Finally, split
in the denominator hints at the connection between the real and imaginary components. Finally, split 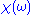 and the equation into their real and imaginary parts to obtain the forms quoted above.
and the equation into their real and imaginary parts to obtain the forms quoted above.
. In physics
, the response function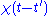 describes how some property
describes how some property 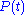 of a physical system responds to a small applied force
of a physical system responds to a small applied force 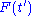 . For example,
. For example, 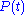 could be the angle
could be the angle
of a pendulum
and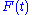 the applied force of a motor
the applied force of a motor
driving the pendulum motion. The response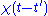 must be zero for
must be zero for 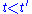 since a system cannot respond to a force before it is applied. It can be shown (for instance, by invoking Titchmarsh's theorem) that this causality condition implies the Fourier transform
since a system cannot respond to a force before it is applied. It can be shown (for instance, by invoking Titchmarsh's theorem) that this causality condition implies the Fourier transform
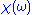 is analytic in the upper half plane.
is analytic in the upper half plane.
Additionally, if we subject the system to an oscillatory force with a frequency much higher than its highest resonant frequency, there will be no time for the system to respond before the forcing has switched direction, and so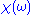 vanishes as
vanishes as  becomes very large. From these physical considerations, we see that
becomes very large. From these physical considerations, we see that 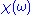 satisfies conditions needed for the Kramers–Kronig relations to apply.
satisfies conditions needed for the Kramers–Kronig relations to apply.
The imaginary part of a response function describes how a system dissipates energy
, since it is out of phase
with the driving force
. The Kramers–Kronig relations imply that observing the dissipative response of a system is sufficient to determine its in-phase (reactive) response, and vice versa.
The formulas above are not useful for reconstructing physical responses, as the integrals run from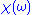 to
to  , implying we know the response at negative frequencies. Fortunately, in most systems, the positive frequency-response determines the negative-frequency response because
, implying we know the response at negative frequencies. Fortunately, in most systems, the positive frequency-response determines the negative-frequency response because 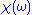 is the Fourier transform of a real quantity
is the Fourier transform of a real quantity 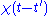 , so
, so 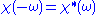 . This means
. This means 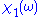 is an even function
is an even function
of frequency and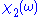 is odd
is odd
.
Using these properties, we can collapse the integration ranges to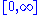 . Consider the first relation giving the real part
. Consider the first relation giving the real part 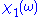 . Transform the integral into one of definite parity by multiplying the numerator and denominator of the integrand by
. Transform the integral into one of definite parity by multiplying the numerator and denominator of the integrand by  and separating:
and separating:
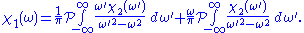
Since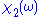 is odd, the second integral vanishes, and we are left with
is odd, the second integral vanishes, and we are left with
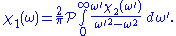
The same derivation for the imaginary part gives
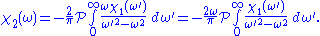
These are the Kramers–Kronig relations useful for physical response functions.
This proof covers slightly different ground from the one above in that it connects the real and imaginary frequency domain parts of any function that is causal in the time domain, and bypasses the condition about the function being analytic in the upper half plane of the frequency domain.
A white paper with an informal, pictorial version of this proof is also available.
, Kramers–Kronig analysis allows one to calculate the energy dependence of both real and imaginary parts of a specimen's light optical permittivity
, together with other optical properties such as the absorption coefficient and reflectivity
.
In short, by measuring the number of high energy (e.g. 200 keV) electrons which lose energy ΔE over a range of energy losses in traversing a very thin specimen (single scattering approximation), one can calculate the energy dependence of permittivity's imaginary part. The dispersion relations allow one to then calculate the energy dependence of the real part.
This measurement is made with electrons, rather than with light, and can be done with very high spatial resolution! One might thereby, for example, look for ultraviolet (UV) absorption bands in a laboratory specimen of interstellar dust less than a 100 nm across, i.e. too small for UV spectroscopy. Although electron spectroscopy has poorer energy resolution than light spectroscopy
, data on properties in visible, ultraviolet and soft x-ray spectral ranges
may be recorded in the same experiment.
In angle resolved photoemission spectroscopy the Kramers-Kronig relations can be used to link the real and imaginary parts of the electrons self energy. This is characteristic of the many body interaction the electron experiences in the material. Notable examples are in the high temperature superconductors, where kinks corresponding to the real part of the self energy are observed in the band dispersion and changes in the MDC width are also observed corresponding to the imaginary part of the self energy.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
relations, connecting the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
parts of any complex function
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
that is analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
in the upper half-plane. These relations are often used to calculate the real part from the imaginary part (or vice versa) of response functions
Linear response function
A linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response...
in physical system
Physical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
s because causality
Causal system
A causal system is a system where the output depends on past/current inputs but not future inputs i.e...
implies the analyticity condition is satisfied, and conversely, analyticity implies causality of the corresponding physical system. The relation is named in honor of Ralph Kronig
Ralph Kronig
Ralph Kronig was a German-American physicist . He is noted for the discovery of particle spin and for his theory of x-ray absorption spectroscopy...
and Hendrik Anthony Kramers
Hendrik Anthony Kramers
Hendrik Anthony "Hans" Kramers was a Dutch physicist.-Background and education:...
.
Definition
Let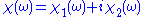 be a complex function of the complex variable
be a complex function of the complex variable  , where
, where 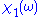 and
and 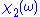 are real
are realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. Suppose this function is analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
in the upper half-plane of
 and it vanishes faster than
and it vanishes faster than 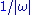 as
as  . The Kramers–Kronig relations are given by
. The Kramers–Kronig relations are given by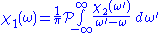
and
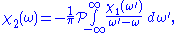
where
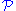 denotes the Cauchy principal value
denotes the Cauchy principal valueCauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
. We see that the real and imaginary parts of such a function are not independent, so that the full function can be reconstructed given just one of its parts.
Derivation
The proof begins with an application of Cauchy's residue theoremResidue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
for complex integration. Given any analytic function
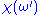 in the upper half plane, the function
in the upper half plane, the function 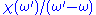 where
where  is real will also be analytic in the upper half of the plane. The residue theorem consequently states that
is real will also be analytic in the upper half of the plane. The residue theorem consequently states that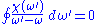

Methods of contour integration
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.Contour integration is closely related to the calculus of residues, a methodology of complex analysis....
within this region. We choose the contour to trace the real axis, a hump over the pole at
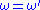 , and a semicircle in the upper half plane at infinity. We then decompose the integral into its contributions along each of these three contour segments. The length of the segment at infinity increases proportionally to
, and a semicircle in the upper half plane at infinity. We then decompose the integral into its contributions along each of these three contour segments. The length of the segment at infinity increases proportionally to  , but its integral component vanishes as long as
, but its integral component vanishes as long as 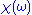 vanishes faster than
vanishes faster than 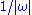 . We are left with the segment along the real axis and the half-circle around the pole:
. We are left with the segment along the real axis and the half-circle around the pole: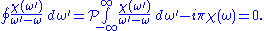
The second term in the middle expression is obtained using the theory of residues. Rearranging, we arrive at the compact form of the Kramers–Kronig relations,
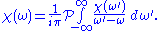
The single
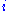 in the denominator hints at the connection between the real and imaginary components. Finally, split
in the denominator hints at the connection between the real and imaginary components. Finally, split 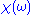 and the equation into their real and imaginary parts to obtain the forms quoted above.
and the equation into their real and imaginary parts to obtain the forms quoted above.Physical interpretation and alternate form
We can apply the Kramers–Kronig formalism to response functionsLinear response function
A linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response...
. In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the response function
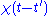 describes how some property
describes how some property 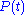 of a physical system responds to a small applied force
of a physical system responds to a small applied force 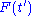 . For example,
. For example, 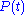 could be the angle
could be the angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
of a pendulum
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
and
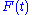 the applied force of a motor
the applied force of a motorActuator
An actuator is a type of motor for moving or controlling a mechanism or system. It is operated by a source of energy, usually in the form of an electric current, hydraulic fluid pressure or pneumatic pressure, and converts that energy into some kind of motion. An actuator is the mechanism by which...
driving the pendulum motion. The response
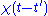 must be zero for
must be zero for 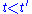 since a system cannot respond to a force before it is applied. It can be shown (for instance, by invoking Titchmarsh's theorem) that this causality condition implies the Fourier transform
since a system cannot respond to a force before it is applied. It can be shown (for instance, by invoking Titchmarsh's theorem) that this causality condition implies the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
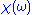 is analytic in the upper half plane.
is analytic in the upper half plane.Additionally, if we subject the system to an oscillatory force with a frequency much higher than its highest resonant frequency, there will be no time for the system to respond before the forcing has switched direction, and so
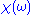 vanishes as
vanishes as  becomes very large. From these physical considerations, we see that
becomes very large. From these physical considerations, we see that 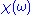 satisfies conditions needed for the Kramers–Kronig relations to apply.
satisfies conditions needed for the Kramers–Kronig relations to apply.The imaginary part of a response function describes how a system dissipates energy
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
, since it is out of phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
with the driving force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
. The Kramers–Kronig relations imply that observing the dissipative response of a system is sufficient to determine its in-phase (reactive) response, and vice versa.
The formulas above are not useful for reconstructing physical responses, as the integrals run from
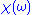 to
to  , implying we know the response at negative frequencies. Fortunately, in most systems, the positive frequency-response determines the negative-frequency response because
, implying we know the response at negative frequencies. Fortunately, in most systems, the positive frequency-response determines the negative-frequency response because 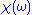 is the Fourier transform of a real quantity
is the Fourier transform of a real quantity 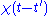 , so
, so 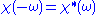 . This means
. This means 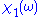 is an even function
is an even functionEven and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
of frequency and
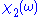 is odd
is oddEven and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
.
Using these properties, we can collapse the integration ranges to
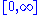 . Consider the first relation giving the real part
. Consider the first relation giving the real part 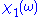 . Transform the integral into one of definite parity by multiplying the numerator and denominator of the integrand by
. Transform the integral into one of definite parity by multiplying the numerator and denominator of the integrand by  and separating:
and separating: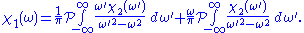
Since
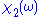 is odd, the second integral vanishes, and we are left with
is odd, the second integral vanishes, and we are left with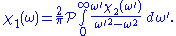
The same derivation for the imaginary part gives
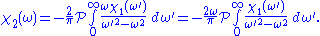
These are the Kramers–Kronig relations useful for physical response functions.
Related proof from the time domain
Hall and Heck give a related and possibly more intuitive proof that avoids contour integration. It is based on the facts that:- Causal impulse responses can be constructed from an even function plus the same function multiplied by the signum functionSign functionIn mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
. - Even and odd part of time domain waveform correspond to real and imaginary parts of its Fourier integral, respectively.
- Multiplication by signum in the time domain corresponds to the Hilbert transformHilbert transformIn mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
(i.e. convolution by the Hilbert kernel) in the frequency domain.
This proof covers slightly different ground from the one above in that it connects the real and imaginary frequency domain parts of any function that is causal in the time domain, and bypasses the condition about the function being analytic in the upper half plane of the frequency domain.
A white paper with an informal, pictorial version of this proof is also available.
Electron spectroscopy
In electron energy loss spectroscopyElectron energy loss spectroscopy
In electron energy loss spectroscopy a material is exposed to a beam of electrons with a known, narrow range of kinetic energies. Some of the electrons will undergo inelastic scattering, which means that they lose energy and have their paths slightly and randomly deflected...
, Kramers–Kronig analysis allows one to calculate the energy dependence of both real and imaginary parts of a specimen's light optical permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
, together with other optical properties such as the absorption coefficient and reflectivity
Reflectivity
In optics and photometry, reflectivity is the fraction of incident radiation reflected by a surface. In general it must be treated as a directional property that is a function of the reflected direction, the incident direction, and the incident wavelength...
.
In short, by measuring the number of high energy (e.g. 200 keV) electrons which lose energy ΔE over a range of energy losses in traversing a very thin specimen (single scattering approximation), one can calculate the energy dependence of permittivity's imaginary part. The dispersion relations allow one to then calculate the energy dependence of the real part.
This measurement is made with electrons, rather than with light, and can be done with very high spatial resolution! One might thereby, for example, look for ultraviolet (UV) absorption bands in a laboratory specimen of interstellar dust less than a 100 nm across, i.e. too small for UV spectroscopy. Although electron spectroscopy has poorer energy resolution than light spectroscopy
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
, data on properties in visible, ultraviolet and soft x-ray spectral ranges
Electromagnetic spectrum
The electromagnetic spectrum is the range of all possible frequencies of electromagnetic radiation. The "electromagnetic spectrum" of an object is the characteristic distribution of electromagnetic radiation emitted or absorbed by that particular object....
may be recorded in the same experiment.
In angle resolved photoemission spectroscopy the Kramers-Kronig relations can be used to link the real and imaginary parts of the electrons self energy. This is characteristic of the many body interaction the electron experiences in the material. Notable examples are in the high temperature superconductors, where kinks corresponding to the real part of the self energy are observed in the band dispersion and changes in the MDC width are also observed corresponding to the imaginary part of the self energy.

