
Kretschmann scalar
Encyclopedia
In the theory of Lorentzian manifolds
, particularly in the context of applications to general relativity
, the Kretschmann scalar is a quadratic scalar invariant
. It was introduced by Erich Kretschmann
.
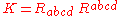
where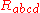 is the Riemann curvature tensor
is the Riemann curvature tensor
. Because it is a sum of squares of tensor components, this is a quadratic invariant.

where is the Weyl tensor
is the Weyl tensor
, the conformal curvature tensor which is also the completely traceless part of the Riemann tensor. In dimensions this is related to the Kretschmann invariant by
dimensions this is related to the Kretschmann invariant by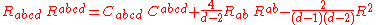
where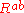 is the Ricci curvature
is the Ricci curvature
tensor and is the Ricci scalar curvature
is the Ricci scalar curvature
(obtained by taking successive traces of the Riemann tensor).
The Kretschmann scalar and the Chern-Pontryagin scalar
where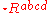 is the left dual of the Riemann tensor, are mathematically analogous (to some extent, physically analogous) to the familiar invariants of the electromagnetic field tensor
is the left dual of the Riemann tensor, are mathematically analogous (to some extent, physically analogous) to the familiar invariants of the electromagnetic field tensor
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, particularly in the context of applications to general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the Kretschmann scalar is a quadratic scalar invariant
Curvature invariant (general relativity)
Curvature invariants in general relativity are a set of scalars called curvature invariants that arise in general relativity. They are formed from the Riemann, Weyl and Ricci tensors - which represent curvature - and possibly operations on them such as contraction, covariant differentiation and...
. It was introduced by Erich Kretschmann
Erich Kretschmann
Erich Justus Kretschmann was a German physicist.He obtained his D.Phil. at Berlin University in 1914 with his dissertation entitled "Eine Theorie der Schwerkraft im Rahmen der ursprünglichen Einsteinschen Relativitätstheorie "...
.
Definition
The Kretschmann invariant is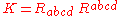
where
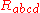 is the Riemann curvature tensor
is the Riemann curvature tensorRiemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
. Because it is a sum of squares of tensor components, this is a quadratic invariant.
Relation to other invariants
Another possible invariant (which has been employed for example in writing the gravitational term of the Lagrangian for some higher-order gravity theories of gravitation) is
where
 is the Weyl tensor
is the Weyl tensorWeyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
, the conformal curvature tensor which is also the completely traceless part of the Riemann tensor. In
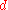 dimensions this is related to the Kretschmann invariant by
dimensions this is related to the Kretschmann invariant by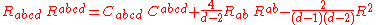
where
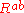 is the Ricci curvature
is the Ricci curvatureRicci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
tensor and
 is the Ricci scalar curvature
is the Ricci scalar curvatureScalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
(obtained by taking successive traces of the Riemann tensor).
The Kretschmann scalar and the Chern-Pontryagin scalar

where
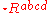 is the left dual of the Riemann tensor, are mathematically analogous (to some extent, physically analogous) to the familiar invariants of the electromagnetic field tensor
is the left dual of the Riemann tensor, are mathematically analogous (to some extent, physically analogous) to the familiar invariants of the electromagnetic field tensor
See also
- Carminati-McLenaghan invariantsCarminati-McLenaghan invariantsIn general relativity, the Carminati–McLenaghan invariants or CM scalars are a set of 16 scalar curvature invariants for the Riemann tensor. This set is usually supplemented with at least two additional invariants.-Mathematical definition:...
, for a set of invariants. - Classification of electromagnetic fieldsClassification of electromagnetic fieldsIn differential geometry and theoretical physics, the classification of electromagnetic fields is a pointwise classification of bivectors at each point of a Lorentzian manifold....
, for more about the invariants of the electromagnetic field tensor. - Curvature invariantCurvature invariantIn Riemannian geometry and pseudo-Riemannian geometry, curvature invariants are scalar quantities constructed from tensors that represent curvature...
, for curvature invariants in Riemannian and pseudo-Riemannian geometry in general. - Curvature invariant (general relativity)Curvature invariant (general relativity)Curvature invariants in general relativity are a set of scalars called curvature invariants that arise in general relativity. They are formed from the Riemann, Weyl and Ricci tensors - which represent curvature - and possibly operations on them such as contraction, covariant differentiation and...
. - Ricci decompositionRicci decompositionIn semi-Riemannian geometry, the Ricci decomposition is a way of breaking up the Riemann curvature tensor of a pseudo-Riemannian manifold into pieces with useful individual algebraic properties...
, for more about the Riemann and Weyl tensor.

