
Kurepa tree
Encyclopedia
In set theory
, a Kurepa tree is a tree
(T, <) of height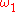 , each of whose levels is at most countable, and has at least
, each of whose levels is at most countable, and has at least 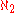 many branches. It was named after Serbian
many branches. It was named after Serbian
mathematician Đuro Kurepa. The existence of a Kurepa tree (known as the Kurepa hypothesis) is independent of the axioms of ZFC. As Solovay
showed, there are Kurepa trees in Gödel
's constructible universe
. On the other hand, as Silver
proved in 1971, if a strongly inaccessible cardinal is Lévy collapsed to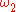 then, in the resulting model, there are no Kurepa trees.
then, in the resulting model, there are no Kurepa trees.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a Kurepa tree is a tree
Tree (set theory)
In set theory, a tree is a partially ordered set In set theory, a tree is a partially ordered set (poset) In set theory, a tree is a partially ordered set (poset) (T, In set theory, a tree is a partially ordered set (poset) (T, ...
(T, <) of height
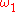 , each of whose levels is at most countable, and has at least
, each of whose levels is at most countable, and has at least 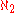 many branches. It was named after Serbian
many branches. It was named after SerbianSerbs
The Serbs are a South Slavic ethnic group of the Balkans and southern Central Europe. Serbs are located mainly in Serbia, Montenegro and Bosnia and Herzegovina, and form a sizable minority in Croatia, the Republic of Macedonia and Slovenia. Likewise, Serbs are an officially recognized minority in...
mathematician Đuro Kurepa. The existence of a Kurepa tree (known as the Kurepa hypothesis) is independent of the axioms of ZFC. As Solovay
Robert M. Solovay
Robert Martin Solovay is an American mathematician specializing in set theory.Solovay earned his Ph.D. from the University of Chicago in 1964 under the direction of Saunders Mac Lane, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem...
showed, there are Kurepa trees in Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
's constructible universe
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
. On the other hand, as Silver
Jack Silver
Jack Howard Silver is a set theorist and logician at the University of California, Berkeley. He has made several deep contributions to set theory...
proved in 1971, if a strongly inaccessible cardinal is Lévy collapsed to
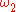 then, in the resulting model, there are no Kurepa trees.
then, in the resulting model, there are no Kurepa trees.

