
Kurosh subgroup theorem
Encyclopedia
In the mathematical
field of group theory
, the Kurosh subgroup theorem describes the algebraic structure of subgroup
s of free product
s of groups
. The theorem was obtained by Alexander Kurosh
, a Russian mathematician, in 1934. Informally, the theorem says that every subgroup of a free product is itself a free product of a free group
and of groups conjugate to the subgroups of the factors of the original free product.
(1958) and others. The theorem was also generalized for describing subgroups of amalgamated free products and HNN extension
s. Other generalizations include considering subgroups of free pro-finite
products and a version of the Kurosh subgroup theorem for topological group
s.
In modern terms, the Kurosh subgroup theorem is a straightforward corollary of the basic structural results of Bass-Serre theory about groups acting
on trees
.
of groups A and B and let H ≤ G be a subgroup
of G. Then there exist a family (Ai)i ∈ I of subgroups Ai ≤ A, a family (Bj)j ∈ J of subgroups Bj ≤ B, families gi, i ∈ I and fj, j ∈ J of elements of G, and a subset X ⊆ G such that
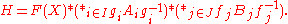
This means that X freely generates
a subgroup of G isomorphic to the free group
F(X) with free basis X and that, moreover, giAigi−1, fjBjfj−1 and X generate
H in G as a free product of the above form.
There is a generalization of this to the case of free products with arbitrarily many factors. Its formulation is:
If H is a subgroup of ∗i∈IGi = G, then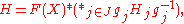
where X ⊆ G and J is some index set and gj ∈ G and each Hj is a subgroup of some Gi.
, as explained, for example in the book of Cohen (1987):
Let G = A∗B and consider G as the fundamental group of a graph of groups
Y consisting of a single non-loop edge with the vertex groups A and B and with the trivial edge group. Let X be the Bass-Serre universal covering tree for the graph of groups Y. Since H ≤ G also acts on X, consider the quotient graph of groups Z for the action of H on X. The vertex groups of Z are subgroups of G-stabilizers of vertices of X, that is, they are conjugate in G to subgroups of A and B. The edge groups of Z are trivial since the G-stabilizers of edges of X were trivial. By the fundamental theorem of Bass–Serre theory, H is canonically isomorphic
to the fundamental group of the graph of groups
Z. Since the edge groups of Z are trivial, it follows that H is equal to the free product of the vertex groups of Z and the free group F(X) which is the fundamental group
(in the standard topological sense) of the underlying graph Z of Z. This implies the conclusion of the Kurosh subgroup theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Kurosh subgroup theorem describes the algebraic structure of subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
s of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. The theorem was obtained by Alexander Kurosh
Aleksandr Gennadievich Kurosh
Aleksandr Gennadievich Kurosh was a Soviet mathematician, known for his work in abstract algebra. He is credited with writing the first modern and high-level text on group theory, his The Theory of Groups published in 1944.He was born in Yartsevo near Smolensk, and died in Moscow. He received his...
, a Russian mathematician, in 1934. Informally, the theorem says that every subgroup of a free product is itself a free product of a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
and of groups conjugate to the subgroups of the factors of the original free product.
History and generalizations
After the original 1934 proof of Kurosh, there were many subsequent proofs of the Kurosh subgroup theorem, including proofs of Kuhn (1952), Mac LaneSaunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
(1958) and others. The theorem was also generalized for describing subgroups of amalgamated free products and HNN extension
HNN extension
In mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
s. Other generalizations include considering subgroups of free pro-finite
Pro-finite group
In mathematics, profinite groups are topological groups that are in a certain sense assembled from finite groups; they share many properties with their finite quotients.- Definition :...
products and a version of the Kurosh subgroup theorem for topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s.
In modern terms, the Kurosh subgroup theorem is a straightforward corollary of the basic structural results of Bass-Serre theory about groups acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
.
Statement of the theorem
Let G = A∗B be the free productFree product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
of groups A and B and let H ≤ G be a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G. Then there exist a family (Ai)i ∈ I of subgroups Ai ≤ A, a family (Bj)j ∈ J of subgroups Bj ≤ B, families gi, i ∈ I and fj, j ∈ J of elements of G, and a subset X ⊆ G such that
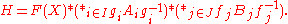
This means that X freely generates
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
a subgroup of G isomorphic to the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
F(X) with free basis X and that, moreover, giAigi−1, fjBjfj−1 and X generate
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
H in G as a free product of the above form.
There is a generalization of this to the case of free products with arbitrarily many factors. Its formulation is:
If H is a subgroup of ∗i∈IGi = G, then
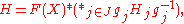
where X ⊆ G and J is some index set and gj ∈ G and each Hj is a subgroup of some Gi.
Proof using Bass-Serre theory
The Kurosh subgroup theorem easily follows from the basic structural results in Bass–Serre theoryBass–Serre theory
Bass–Serre theory is a part of the mathematical subject of group theory that deals with analyzing the algebraic structure of groups acting by automorphisms on simplicial trees...
, as explained, for example in the book of Cohen (1987):
Let G = A∗B and consider G as the fundamental group of a graph of groups
Graph of groups
In geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
Y consisting of a single non-loop edge with the vertex groups A and B and with the trivial edge group. Let X be the Bass-Serre universal covering tree for the graph of groups Y. Since H ≤ G also acts on X, consider the quotient graph of groups Z for the action of H on X. The vertex groups of Z are subgroups of G-stabilizers of vertices of X, that is, they are conjugate in G to subgroups of A and B. The edge groups of Z are trivial since the G-stabilizers of edges of X were trivial. By the fundamental theorem of Bass–Serre theory, H is canonically isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the fundamental group of the graph of groups
Graph of groups
In geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
Z. Since the edge groups of Z are trivial, it follows that H is equal to the free product of the vertex groups of Z and the free group F(X) which is the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
(in the standard topological sense) of the underlying graph Z of Z. This implies the conclusion of the Kurosh subgroup theorem.
See also
- HNN extensionHNN extensionIn mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
- Bass-Serre theory
- Graph of groupsGraph of groupsIn geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
- Geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...

