Kuznetsov trace formula
Encyclopedia
In analytic number theory
, the Kuznetsov trace formula is an extension of the Petersson trace formula
introduced in
.
The Kuznetsov or relative trace formula connects Kloosterman sums at a deep level with the spectral theory of automorphic form
s. Originally this could have been stated as follows. Let
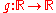
be a sufficiently "well behaved" function. Then one calls identities of the following type Kuznetsov trace formula:
The integral transform part is some integral transform of g and the spectral part is a sum of Fourier coefficients, taken over spaces of holomorphic and non-holomorphic modular forms twisted with some integral transform of g. The Kuznetsov trace formula was found by Kuznetsov while studying the growth of weight zero automorphic functions. Using estimates on Kloosterman sums he was able to derive estimates for Fourier coefficients of modular forms in cases where Pierre Deligne
's proof of the Weil conjectures
was not applicable.
It was later translated by Jacquet to a representation theoretic
framework. Let
be a reductive group
over a number field F and
be a subgroup. While the usual trace formula
studies the harmonic analysis
on G, the relative trace formula a tool for studying the harmonic analysis on the symmetric space
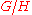. For an overview and numerous applications Cogdell, J.W. and I. Piatetski-Shapiro, The arithmetic and spectral analysis of Poincaré series, volume 13 of Perspectives in mathematics. Academic Press Inc., Boston, MA, (1990).
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
, the Kuznetsov trace formula is an extension of the Petersson trace formula
Petersson trace formula
In analytic number theory, the Petersson trace formula is a kind of orthogonality relation between coefficients of a holomorphic modular form. It is a specialization of the more general Kuznetsov trace formula....
introduced in
.
The Kuznetsov or relative trace formula connects Kloosterman sums at a deep level with the spectral theory of automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s. Originally this could have been stated as follows. Let
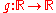
be a sufficiently "well behaved" function. Then one calls identities of the following type Kuznetsov trace formula:
The integral transform part is some integral transform of g and the spectral part is a sum of Fourier coefficients, taken over spaces of holomorphic and non-holomorphic modular forms twisted with some integral transform of g. The Kuznetsov trace formula was found by Kuznetsov while studying the growth of weight zero automorphic functions. Using estimates on Kloosterman sums he was able to derive estimates for Fourier coefficients of modular forms in cases where Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
's proof of the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
was not applicable.
It was later translated by Jacquet to a representation theoretic
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
framework. Let
be a reductive groupReductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
over a number field F and
be a subgroup. While the usual trace formulaSelberg trace formula
In mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...
studies the harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
on G, the relative trace formula a tool for studying the harmonic analysis on the symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
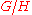. For an overview and numerous applications Cogdell, J.W. and I. Piatetski-Shapiro, The arithmetic and spectral analysis of Poincaré series, volume 13 of Perspectives in mathematics. Academic Press Inc., Boston, MA, (1990).