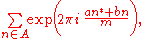Kloosterman sum
Encyclopedia
In mathematics
, a Kloosterman sum is a particular kind of exponential sum
. Let a, b, m be natural numbers. Then
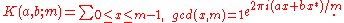
Here x* is the inverse of x modulo
m. They are named for the Dutch mathematician Hendrik Kloosterman
, who introduced them in 1926 when he adapted the Hardy-Littlewood circle method
to tackle a problem involving positive definite diagonal quadratic form
s in four as opposed to five or more variables, which he had dealt with in his dissertation in 1924.
analogue of Bessel function
s. They occur (for example) in the Fourier expansion of modular forms.
There are applications to mean values involving the Riemann zeta function, primes
in short intervals, primes in arithmetic progressions, the spectral theory of automorphic functions and related topics.
This identity was first stated by Atle Selberg
and first proved by Kuznetsov by using the spectral theory
of modular forms. Nowadays elementary proofs of this identity are known.
The symbol denotes the Jacobi symbol
denotes the Jacobi symbol
.

Here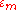 for odd m is defined to be 1 if
for odd m is defined to be 1 if  and
and  if
if  and
and 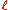 is chosen in such a way that
is chosen in such a way that  . This formula was first found by Hans Salie and there are many simple proofs in the literature.
. This formula was first found by Hans Salie and there are many simple proofs in the literature.
and states:
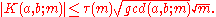
Here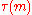 is the number of positive divisors of
is the number of positive divisors of  . Because of the multiplicative properties of Kloosterman sums these estimates may be reduced to the case where m is a prime number p. A fundamental technique of Weil reduces the estimate
. Because of the multiplicative properties of Kloosterman sums these estimates may be reduced to the case where m is a prime number p. A fundamental technique of Weil reduces the estimate
when ab ≠ 0 to his results on local zeta-function
s. Geometrically the sum is taken along a 'hyperbola'
and we consider this as defining an algebraic curve
over the finite field with p elements. This curve has a ramified Artin-Schreier covering C, and Weil showed that the local zeta-function of C has a factorization; this is the Artin L-function
theory for the case of global field
s that are function fields, for which Weil gives a 1938 paper of J. Weissinger as reference (the next year he gave a 1935 paper of Hasse
as earlier reference for the idea; given Weil's rather denigratory remark on the abilities of analytic number theorists to work out this example themselves, in his Collected Papers, these ideas were presumably 'folklore' of quite long standing). The non-polar factors are of type
where K is a Kloosterman sum. The estimate then follows from Weil's basic work of 1940.
This technique in fact shows much more generally that complete exponential sums 'along' algebraic varieties have good estimates, depending on the Weil conjectures
in dimension > 1. It has been pushed much further by Pierre Deligne
, Gérard Laumon
, and Nicholas Katz.
where runs through a set
runs through a set  of numbers, coprime to
of numbers, coprime to  , the number of elements
, the number of elements  in which is essentially smaller than
in which is essentially smaller than  , and the symbol
, and the symbol  denotes the congruence class, inverse to
denotes the congruence class, inverse to  modulo
modulo  :
:  .
.
Up to the early 1990s, estimates for sums of this type were known mainly in the case where the number of summands was greater than . Such estimates were due to H. D. Kloosterman
. Such estimates were due to H. D. Kloosterman
, I. M. Vinogradov
, H. Salie,
L. Carlitz
, S. Uchiyama and A. Weil
. The only exceptions were the special modules of the form , where
, where 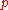 is a fixed prime and the exponent
is a fixed prime and the exponent  increases to infinity (this case was studied by A.G. Postnikov by means of the method of Ivan Matveyevich Vinogradov
increases to infinity (this case was studied by A.G. Postnikov by means of the method of Ivan Matveyevich Vinogradov
).
In the 1990s Anatolii Alexeevitch Karatsuba
developed a new method of estimating short Kloosterman sums. Karatsuba's method makes it possible to estimate Kloosterman's sums, the number of summands in which does not exceed , and in some cases even
, and in some cases even  , where
, where  is an arbitrarily small fixed number. The last paper of A.A. Karatsuba on this subject was published after his death.
is an arbitrarily small fixed number. The last paper of A.A. Karatsuba on this subject was published after his death.
Various aspects of the method of Karatsuba found applications in solving the following problems of analytic number theory:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Kloosterman sum is a particular kind of exponential sum
Exponential sum
In mathematics, an exponential sum may be a finite Fourier series , or other finite sum formed using the exponential function, usually expressed by means of the functione = \exp.\,...
. Let a, b, m be natural numbers. Then
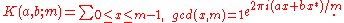
Here x* is the inverse of x modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
m. They are named for the Dutch mathematician Hendrik Kloosterman
Hendrik Kloosterman
Hendrik Douwe Kloosterman was a Dutch mathematician, known for his work in number theory and in representation theory....
, who introduced them in 1926 when he adapted the Hardy-Littlewood circle method
Hardy-Littlewood circle method
In mathematics, the Hardy–Littlewood circle method is one of the most frequently used techniques of analytic number theory. It is named for G. H. Hardy and J. E...
to tackle a problem involving positive definite diagonal quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s in four as opposed to five or more variables, which he had dealt with in his dissertation in 1924.
Context
The Kloosterman sums are a finite ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
analogue of Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s. They occur (for example) in the Fourier expansion of modular forms.
There are applications to mean values involving the Riemann zeta function, primes
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
in short intervals, primes in arithmetic progressions, the spectral theory of automorphic functions and related topics.
Properties of the Kloosterman sums
- The Kloosterman sum K(a,b; m) depends only on the residue class of a,b modulo m. Furthermore K(a,b;m)=K(b,a,m) and K(ac,b;m)=K(a,bc,m) if gcd(c,m)=1. The value of
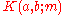 is always an algebraic real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
is always an algebraic real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. In fact K(a,b; m) is an element of the subfield which is the compositum of the fields
which is the compositum of the fields 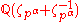 for all odd primes p with
for all odd primes p with  and
and 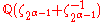 for
for 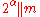 with
with  .
.
- If a=0 or b=0 then the Kloosterman sum reduces to the Ramanujan sum.
- Let
 with coprime
with coprime 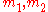 . Choose
. Choose  with
with 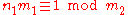 and
and 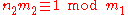 . Then
. Then 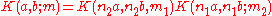 . This reduces the evaluation of Kloosterman sums to the case where
. This reduces the evaluation of Kloosterman sums to the case where  for a prime number p and an integer
for a prime number p and an integer  .
.
- We have the Selberg identity
This identity was first stated by Atle Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
and first proved by Kuznetsov by using the spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
of modular forms. Nowadays elementary proofs of this identity are known.
- Let m=p with p be an odd prime. Then no simple formula of K(a,b;m) is known and the Sato-Tate conjectureSato-Tate conjectureIn mathematics, the Sato–Tate conjecture is a statistical statement about the family of elliptic curves Ep over the finite field with p elements, with p a prime number, obtained from an elliptic curve E over the rational number field, by the process of reduction modulo a prime for almost all p...
suggests that none exists. The lifting formulas below, however, are often as good as an explicit evaluation. If gcd(a,p)=1 one furthermore has the important transformation:
The symbol
 denotes the Jacobi symbol
denotes the Jacobi symbolJacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
.
- Let
 with k>1, p prime and assume
with k>1, p prime and assume 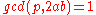 . Then K(a,b;m) = 0 unless
. Then K(a,b;m) = 0 unless 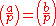 in which case
in which case

Here
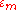 for odd m is defined to be 1 if
for odd m is defined to be 1 if  and
and 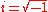 if
if  and
and 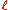 is chosen in such a way that
is chosen in such a way that  . This formula was first found by Hans Salie and there are many simple proofs in the literature.
. This formula was first found by Hans Salie and there are many simple proofs in the literature.Estimates
Because Kloosterman sums occur in the Fourier expansion of modular forms, estimates for Kloosterman sums yield estimates for Fourier coefficients of modular forms as well. The most famous estimate is due to André WeilAndré Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
and states:
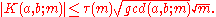
Here
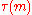 is the number of positive divisors of
is the number of positive divisors of  . Because of the multiplicative properties of Kloosterman sums these estimates may be reduced to the case where m is a prime number p. A fundamental technique of Weil reduces the estimate
. Because of the multiplicative properties of Kloosterman sums these estimates may be reduced to the case where m is a prime number p. A fundamental technique of Weil reduces the estimate- |K(a,b;p)| ≤ 2√p
when ab ≠ 0 to his results on local zeta-function
Local zeta-function
In number theory, a local zeta-functionis a function whose logarithmic derivative is a generating functionfor the number of solutions of a set of equations defined over a finite field F, in extension fields Fk of F.-Formulation:...
s. Geometrically the sum is taken along a 'hyperbola'
- XY = ab
and we consider this as defining an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
over the finite field with p elements. This curve has a ramified Artin-Schreier covering C, and Weil showed that the local zeta-function of C has a factorization; this is the Artin L-function
Artin L-function
In mathematics, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group G. These functions were introduced in the 1923 by Emil Artin, in connection with his research into class field theory. Their fundamental properties, in particular the Artin...
theory for the case of global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s that are function fields, for which Weil gives a 1938 paper of J. Weissinger as reference (the next year he gave a 1935 paper of Hasse
Helmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
as earlier reference for the idea; given Weil's rather denigratory remark on the abilities of analytic number theorists to work out this example themselves, in his Collected Papers, these ideas were presumably 'folklore' of quite long standing). The non-polar factors are of type
- 1 − Kt
where K is a Kloosterman sum. The estimate then follows from Weil's basic work of 1940.
This technique in fact shows much more generally that complete exponential sums 'along' algebraic varieties have good estimates, depending on the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
in dimension > 1. It has been pushed much further by Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
, Gérard Laumon
Gérard Laumon
Gérard Laumon is a French mathematician. He studied at the École Normale Supérieure and Paris-Sud 11 University, Orsay.In 2004 Laumon and Ngô Bảo Châu received the Clay Research Award for the proof of the Langlands and Shelstad's Fundamental Lemma for unitary groups, a key component in the...
, and Nicholas Katz.
Short Kloosterman sums
Short Kloosterman sums are defined as trigonometric sums of the formwhere
 runs through a set
runs through a set  of numbers, coprime to
of numbers, coprime to  , the number of elements
, the number of elements  in which is essentially smaller than
in which is essentially smaller than  , and the symbol
, and the symbol  denotes the congruence class, inverse to
denotes the congruence class, inverse to  modulo
modulo  :
:  .
.Up to the early 1990s, estimates for sums of this type were known mainly in the case where the number of summands was greater than
 . Such estimates were due to H. D. Kloosterman
. Such estimates were due to H. D. KloostermanHendrik Kloosterman
Hendrik Douwe Kloosterman was a Dutch mathematician, known for his work in number theory and in representation theory....
, I. M. Vinogradov
Ivan Matveyevich Vinogradov
Ivan Matveevich Vinogradov was a Soviet mathematician, who was one of the creators of modern analytic number theory, and also a dominant figure in mathematics in the USSR. He was born in the Velikiye Luki district, Pskov Oblast. He graduated from the University of St...
, H. Salie,
L. Carlitz
Leonard Carlitz
Leonard Carlitz was an American mathematician. Carlitz supervised 44 Doctorates at Duke University and published over 770 papers.- Chronology :* 1907 Born Philadelphia, PA, USA* 1927 BA, University of Pennsylvania...
, S. Uchiyama and A. Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
. The only exceptions were the special modules of the form
 , where
, where 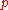 is a fixed prime and the exponent
is a fixed prime and the exponent  increases to infinity (this case was studied by A.G. Postnikov by means of the method of Ivan Matveyevich Vinogradov
increases to infinity (this case was studied by A.G. Postnikov by means of the method of Ivan Matveyevich VinogradovIvan Matveyevich Vinogradov
Ivan Matveevich Vinogradov was a Soviet mathematician, who was one of the creators of modern analytic number theory, and also a dominant figure in mathematics in the USSR. He was born in the Velikiye Luki district, Pskov Oblast. He graduated from the University of St...
).
In the 1990s Anatolii Alexeevitch Karatsuba
Anatolii Alexeevitch Karatsuba
Anatolii Alexeevitch Karatsuba was a Russian mathematician, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers.- Studies and work :...
developed a new method of estimating short Kloosterman sums. Karatsuba's method makes it possible to estimate Kloosterman's sums, the number of summands in which does not exceed
 , and in some cases even
, and in some cases even  , where
, where  is an arbitrarily small fixed number. The last paper of A.A. Karatsuba on this subject was published after his death.
is an arbitrarily small fixed number. The last paper of A.A. Karatsuba on this subject was published after his death.Various aspects of the method of Karatsuba found applications in solving the following problems of analytic number theory:
- finding asymptotics of the sums of fractional parts of the form :
 : where
: where  runs, one after another, through the integers satisfying the condition
runs, one after another, through the integers satisfying the condition 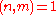 , and
, and  runs through the primes that do not divide the module
runs through the primes that do not divide the module  (A.A.Karatsuba);
(A.A.Karatsuba);
- finding the lower bound for the number of solutions of the inequalities of the form :
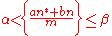 : in the integers
: in the integers  ,
,  , coprime to
, coprime to  ,
,  (A.A. Karatsuba);
(A.A. Karatsuba);
- the precision of approximation of an arbitrary real number in the segment
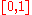 by fractional parts of the form :
by fractional parts of the form :
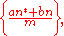 : where
: where  ,
, 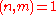 ,
, 
(A.A. Karatsuba);
- a more precise constant
 in the Brun–Titchmarsh theoremBrun–Titchmarsh theoremIn analytic number theory, the Brun–Titchmarsh theorem, named after Viggo Brun and Edward Charles Titchmarsh, is an upper bound on the distribution of prime numbers in arithmetic progression...
in the Brun–Titchmarsh theoremBrun–Titchmarsh theoremIn analytic number theory, the Brun–Titchmarsh theorem, named after Viggo Brun and Edward Charles Titchmarsh, is an upper bound on the distribution of prime numbers in arithmetic progression...
:
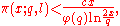 : where
: where 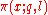 is the number of primes
is the number of primes 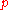 , not exceeding
, not exceeding  and belonging to the arithmetic progression
and belonging to the arithmetic progression 
(J. FriedlanderJohn FriedlanderJohn Benjamin Friedlander is a Canadian mathematician specializing in analytic number theory. He received his B.Sc. from the University of Toronto in 1965, an M.A. from the University of Waterloo in 1966, and a Ph.D. from Pennsylvania State University in 1972. He was a lecturer at M.I.T...
, H. IwaniecHenryk IwaniecHenryk Iwaniec is a Polish American mathematician, and since 1987 a professor at Rutgers University. He was awarded the fourteenth Frank Nelson Cole Prize in Number Theory in 2002. He received the Leroy P. Steele Prize for Mathematical Exposition in 2011.-Background and education:Iwaniec studied...
);
- a lower bound for the greatest prime divisor of the product of numbers of the form :
 ,
, 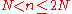
(D. R. Heath-BrownRoger Heath-BrownDavid Rodney "Roger" Heath-Brown F.R.S. , is a British mathematician working in the field of analytic number theory. He was an undergraduate and graduate student of Trinity College, Cambridge; his research supervisor was Alan Baker...
);
- proving that there are infinitely many primes of the form :

(J. FriedlanderJohn FriedlanderJohn Benjamin Friedlander is a Canadian mathematician specializing in analytic number theory. He received his B.Sc. from the University of Toronto in 1965, an M.A. from the University of Waterloo in 1966, and a Ph.D. from Pennsylvania State University in 1972. He was a lecturer at M.I.T...
, H. IwaniecHenryk IwaniecHenryk Iwaniec is a Polish American mathematician, and since 1987 a professor at Rutgers University. He was awarded the fourteenth Frank Nelson Cole Prize in Number Theory in 2002. He received the Leroy P. Steele Prize for Mathematical Exposition in 2011.-Background and education:Iwaniec studied...
);
- combinatorial properties of the set of numbers :


(A.A.Glibichuk).
Lifting of Kloosterman sums
Although the Kloosterman sums may not be calculated in general they may be "lifted" to algebraic number fields, which often yields more convenient formulas. Let be a squarefree integer with
be a squarefree integer with  . Assume that for any prime factor p of m we have
. Assume that for any prime factor p of m we have 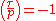 . Then for all integers a,b coprime to m we have
. Then for all integers a,b coprime to m we have
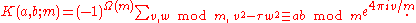
Here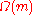 is the number of prime factors of m counting multiplicity.The sum on the right can be reinterpreted as a sum over algebraic integers in the field
is the number of prime factors of m counting multiplicity.The sum on the right can be reinterpreted as a sum over algebraic integers in the field 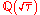 . This formula is due to Yangbo Ye, inspired by Don ZagierDon ZagierDon Bernard Zagier is an American mathematician whose main area of work is number theory. He is currently one of the directors of the Max Planck Institute for Mathematics in Bonn, Germany, and a professor at the Collège de France in Paris, France.He was born in Heidelberg, Germany...
. This formula is due to Yangbo Ye, inspired by Don ZagierDon ZagierDon Bernard Zagier is an American mathematician whose main area of work is number theory. He is currently one of the directors of the Max Planck Institute for Mathematics in Bonn, Germany, and a professor at the Collège de France in Paris, France.He was born in Heidelberg, Germany...
and extending the work of Hervé JacquetHervé JacquetHervé Jacquet is a French American mathematician born in France in 1939, working in automorphic forms. He is considered one of the founders of the theory of automorphic representations and their associated L-functions, and his results play a central role in modern number theory.-Career:Jacquet...
and Ye on the relative trace formulaSelberg trace formulaIn mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...
for . Indeed, much more general exponential sums can be lifted.
. Indeed, much more general exponential sums can be lifted.
Kuznetsov trace formula
The Kuznetsov or relative trace formula connects Kloosterman sums at a deep level with the spectral theory of automorphic formAutomorphic formIn mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s. Originally this could have been stated as follows. Let
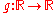
be a sufficiently "well behaved" function. Then one calls identities of the following type Kuznetsov trace formula:

The integral transform part is some integral transform of g and the spectral part is a sum of Fourier coefficients, taken over spaces of holomorphic and non-holomorphic modular forms twisted with some integral transform of g. The Kuznetsov trace formula was found by Kuznetsov while studying the growth of weight zero automorphic functions. Using estimates on Kloosterman sums he was able to derive estimates for Fourier coefficients of modular forms in cases where Pierre DelignePierre Deligne- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
's proof of the Weil conjecturesWeil conjecturesIn mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
was not applicable.
It was later translated by Jacquet to a representation theoreticRepresentation theoryRepresentation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
framework. Let be a reductive groupReductive groupIn mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
be a reductive groupReductive groupIn mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
over a number field F and be a subgroup. While the usual trace formulaSelberg trace formulaIn mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...
be a subgroup. While the usual trace formulaSelberg trace formulaIn mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...
studies the harmonic analysisHarmonic analysisHarmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
on G, the relative trace formula a tool for studying the harmonic analysis on the symmetric spaceSymmetric spaceA symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
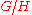 . For an overview and numerous applications see the references.
. For an overview and numerous applications see the references.
History
Weil's estimate can now be studied in W. M. Schmidt, Equations over finite fields: an elementary approach, 2nd. edn. (Kendrick Press, 2004). The underlying ideas here are due to S. Stepanov and draw inspiration from Axel ThueAxel ThueAxel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....
's work in Diophantine approximationDiophantine approximationIn number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
.
There are many connections between Kloosterman sums and modular formModular formIn mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s. In fact the sums first appeared (minus the name) in a 1912 paper of Henri PoincaréHenri PoincaréJules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
on modular forms. Hans Salie introduced a form of Kloosterman sum that is twisted by a Dirichlet characterDirichlet characterIn number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
: such Salie sums have an elementary evaluation.
After the discovery of important formulae connecting Kloosterman sums with non-holomorphic modular forms by KuznetsovKuznetsovKuznetsov, Kuznyetsov, or Kuznetsoff or Kuznetsova is the third most common Russian surname, an equivalent of the English "Smith" ....
in 1979, which contained some 'savings on average' over the square root estimate, there were further developments by Iwaniec and Deshouillers in a seminal paper in Inventiones MathematicaeInventiones MathematicaeInventiones Mathematicae, often just referred to as Inventiones, is a mathematical journal published monthly by Springer Verlag. It was founded in 1966.-Editors:...
(1982). Subsequent applications to analytic number theory were worked out by a number of authors, particularly Enrico BombieriEnrico BombieriEnrico Bombieri is a mathematician who has been working at the Institute for Advanced Study in Princeton, New Jersey. Bombieri's research in number theory, algebraic geometry, and mathematical analysis have earned him many international prizes --- a Fields Medal in 1974 and the Balzan Prize in 1980...
, Fouvry, Friedlander and Iwaniec.
The field remains somewhat inaccessible. A detailed introduction to the spectral theorySpectral theoryIn mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
needed to understand the Kuznetsov formulae is given in R. C. Baker, Kloosterman Sums and Maass Forms, vol. I (Kendrick press, 2003). Also relevant for students and researchers interested in the field is H. Iwaniec and E. Kowalski, Analytic Number Theory (American Mathematical Society). - finding the lower bound for the number of solutions of the inequalities of the form :