
Petersson trace formula
Encyclopedia
In analytic number theory
, the Petersson trace formula is a kind of orthogonality relation between coefficients of a holomorphic modular form
. It is a specialization of the more general Kuznetsov trace formula.
In its simplest form the Petersson trace formula is as follows. Let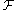 be an orthonormal basis of
be an orthonormal basis of 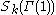 , the space of cusp forms of weight
, the space of cusp forms of weight  on
on 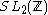 . Then for any positive integers
. Then for any positive integers  we have
we have
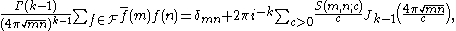
where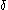 is the Kronecker delta function,
is the Kronecker delta function, 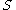 is the Kloosterman sum and
is the Kloosterman sum and 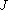 is the Bessel function
is the Bessel function
of the first kind.
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
, the Petersson trace formula is a kind of orthogonality relation between coefficients of a holomorphic modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
. It is a specialization of the more general Kuznetsov trace formula.
In its simplest form the Petersson trace formula is as follows. Let
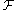 be an orthonormal basis of
be an orthonormal basis of 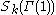 , the space of cusp forms of weight
, the space of cusp forms of weight  on
on 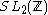 . Then for any positive integers
. Then for any positive integers  we have
we have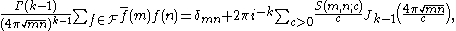
where
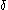 is the Kronecker delta function,
is the Kronecker delta function, 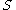 is the Kloosterman sum and
is the Kloosterman sum and 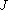 is the Bessel function
is the Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind.

