Ladder operator
Encyclopedia
In linear algebra
(and its application to quantum mechanics
), a raising or lowering operator (collectively known as ladder operators) is an operator that increases or decreases the eigenvalue of another operator. In quantum mechanics, the raising operator is sometimes called the creation operator, and the lowering operator the annihilation operator. Well-known applications of ladder operators in quantum mechanics are in the formalisms of the quantum harmonic oscillator
and angular momentum
.
.
Many sources credit Dirac with the original invention of ladder operators. Dirac's use of the ladder operators goes as far as to show that the total angular momentum quantum number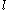
, or actually 
, needs to be a non-negative half integer multiple of ħ. He also showed how the magnetic quantum number
needs to run from 
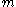to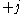 
in integer steps of ħ. However, this is too general because 
is related to a rotation about the z-axis. It is inconceivable that a full rotation does not return a system to itself (which is the reason the introduction of spin-½
was resisted at first). In order for a full rotation to return a system to itself,
must be an integer multiple of ħ, not just half-integer. In order to account for this, we split the total angular momentum of the electron into the orbital component 
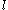, which must obey the intuitive requirements of full rotation, and the intrinsic spin component 
, which is not required to do so. Once this split is made, we can easily apply physical intuition to the problem. The results, then, are in agreement with experiment.
The restriction on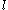
and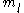 
to integer multiples of ħ was done by "H. E. Rorschach at the 1962 Southwestern Meeting of the American Physical Society." There is also resistance to such a split, so that, in the same year, Merzbacher derived the same boundary conditions from another angle of attack, the Aharonov-Bohm effect
. The arguments and ladder operators themselves have been extended many times since, to deal with spin, and to generate more than just m for given l, but also to generate l.
. The creation operator ai† increments the number of particles in state i, while the corresponding annihilation operator ai decrements the number of particles in state i. This clearly satisfies the requirements of the above definition of a ladder operator: the incrementing or decrementing of the eigenvalue of another operator (in this case the particle number operator
).
Confusion arises because the term ladder operator is typically used to describe an operator that acts to increment or decrement a quantum number
describing the state of a system. To change the state of a particle with creation/annihilation operators requires the use of an annihilation operator to remove a particle from the initial state and a creation operator to add a particle to the final state.
for some scalar c. If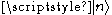
is an eigenstate of N with eigenvalue equation,
then the operator X acts on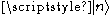
in such a way as to shift the eigenvalue by c:
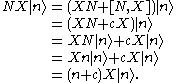
In other words, if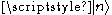
is an eigenstate of N with eigenvalue n then 
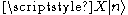is an eigenstate of N with eigenvalue n + c. The operator X is a raising operator for N if c is real and positive, and a lowering operator for N if c is real and negative.
If N is a Hermitian operator then c must be real and the Hermitian adjoint
of X obeys the commutation relation:
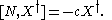
In particular, if X is a lowering operator for N then X† is a raising operator for N and vice-versa.
treatment of angular momentum
. For a general angular momentum vector, J, with components, Jx, Jy and Jz we define the two ladder operators, J+ and J-:
where i is the imaginary unit
.
The commutation relation between the cartesian
components of any angular momentum operator is given by
where εijk is the Levi-Civita symbol
and each of i, j and k can take any of the values x, y and z. From this the commutation relations between the ladder operators and Jz can easily be obtained:
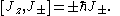
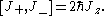
The properties of the ladder operators can be determined by observing how they modify the action of the Jz operator on a given state:
Compare this result with:
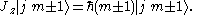
Thus we conclude that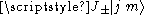
is some scalar
multiplied by
,
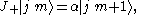
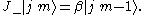
This illustrates the defining feature of ladder operators in quantum mechanics: the incrementing (or decrementing) of a quantum number, thus mapping one quantum state onto another. This is the reason that they are often known as raising and lowering operators.
To obtain the values of α and β we first take the norm of each operator, recognizing that J+ and J- are a Hermitian conjugate pair (
),
,
.
The product of the ladder operators can be expressed in terms of the commuting pair J2 and Jz,
Thus we can express the values of |α|2 and |β|2 in terms of the eigenvalues of J2 and Jz,
The phases
of α and β are not physically significant, thus they can be chosen to be real
and we have:
Confirming that m is bounded by the value of j (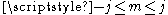
) we have:
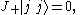
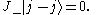
Angular momentum algebra can often be simplified by recasting it in the spherical basis. Using the notation of spherical tensor operators, the "-1", "0" and "+1" components of J(1) ≡ J are given by,
From these definitions it can be shown that the above scalar product can be expanded as
The significance of this expansion is that it clearly indicates which states are coupled by this term in the Hamiltonian, that is those with quantum numbers differing by mi = ±1 and mj = 1 only.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
(and its application to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
), a raising or lowering operator (collectively known as ladder operators) is an operator that increases or decreases the eigenvalue of another operator. In quantum mechanics, the raising operator is sometimes called the creation operator, and the lowering operator the annihilation operator. Well-known applications of ladder operators in quantum mechanics are in the formalisms of the quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
.
Theoretical Significance and History
Quantum mechanics is concerned with discreteness, of which angular momentum eigenstates of the atoms must also be. Raising and lowering operators serve as relations between these discrete states. It has some practical uses as shorthand methods to generate possible states from given states. However, they have much deeper implications for theoretical applications because they can be used to theoretically show that discreteness of angular momentum exists even in classical physics. Since the rigorous quantum mechanics of Heisenberg and Schroedinger are all that are required to derive these ladder operators, they can be used to show the superiority of formalised quantum mechanics over old quantum theoryOld quantum theory
The old quantum theory was a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was a collection of heuristic prescriptions which are now understood to be the first quantum corrections to classical mechanics...
.
Many sources credit Dirac with the original invention of ladder operators. Dirac's use of the ladder operators goes as far as to show that the total angular momentum quantum number
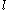, or actually , needs to be a non-negative half integer multiple of ħ. He also showed how the magnetic quantum numberMagnetic quantum number
In atomic physics, the magnetic quantum number is the third of a set of quantum numbers which describe the unique quantum state of an electron and is designated by the letter m...
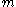needs to run from to 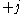in integer steps of ħ. However, this is too general because is related to a rotation about the z-axis. It is inconceivable that a full rotation does not return a system to itself (which is the reason the introduction of spin-½Spin-½
In quantum mechanics, spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.- Overview :Particles...
was resisted at first). In order for a full rotation to return a system to itself,
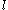must be an integer multiple of ħ, not just half-integer. In order to account for this, we split the total angular momentum of the electron into the orbital component , which must obey the intuitive requirements of full rotation, and the intrinsic spin component , which is not required to do so. Once this split is made, we can easily apply physical intuition to the problem. The results, then, are in agreement with experiment.The restriction on
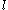and 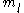to integer multiples of ħ was done by "H. E. Rorschach at the 1962 Southwestern Meeting of the American Physical Society." There is also resistance to such a split, so that, in the same year, Merzbacher derived the same boundary conditions from another angle of attack, the Aharonov-Bohm effectAharonov-Bohm effect
The Aharonov–Bohm effect, sometimes called the Ehrenberg–Siday–Aharonov–Bohm effect, is a quantum mechanical phenomenon in which an electrically charged particle is affected by an electromagnetic field , despite being confined to a region in which both the magnetic field B and electric field E are...
. The arguments and ladder operators themselves have been extended many times since, to deal with spin, and to generate more than just m for given l, but also to generate l.
Terminology
There is some confusion regarding the relationship between the raising and lowering ladder operators and the creation and annihilation operators commonly used in quantum field theoryQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. The creation operator ai† increments the number of particles in state i, while the corresponding annihilation operator ai decrements the number of particles in state i. This clearly satisfies the requirements of the above definition of a ladder operator: the incrementing or decrementing of the eigenvalue of another operator (in this case the particle number operator
Particle number operator
In quantum mechanics, for systems where the total number of particles may not be preserved, the number operator is the observable that counts the number of particles.The number operator acts on Fock space...
).
Confusion arises because the term ladder operator is typically used to describe an operator that acts to increment or decrement a quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
describing the state of a system. To change the state of a particle with creation/annihilation operators requires the use of an annihilation operator to remove a particle from the initial state and a creation operator to add a particle to the final state.
General formulation
Suppose that two operators X and N have the commutation relation,for some scalar c. If
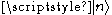is an eigenstate of N with eigenvalue equation,then the operator X acts on
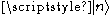in such a way as to shift the eigenvalue by c: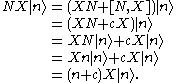In other words, if
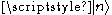is an eigenstate of N with eigenvalue n then 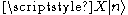is an eigenstate of N with eigenvalue n + c. The operator X is a raising operator for N if c is real and positive, and a lowering operator for N if c is real and negative.If N is a Hermitian operator then c must be real and the Hermitian adjoint
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of X obeys the commutation relation:
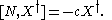
In particular, if X is a lowering operator for N then X† is a raising operator for N and vice-versa.
Angular momentum
A particular application of the ladder operator concept is found in the quantum mechanicalQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
treatment of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. For a general angular momentum vector, J, with components, Jx, Jy and Jz we define the two ladder operators, J+ and J-:
where i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
The commutation relation between the cartesian
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
components of any angular momentum operator is given by
where εijk is the Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
and each of i, j and k can take any of the values x, y and z. From this the commutation relations between the ladder operators and Jz can easily be obtained:
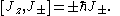
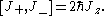
The properties of the ladder operators can be determined by observing how they modify the action of the Jz operator on a given state:
Compare this result with:
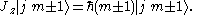
Thus we conclude that
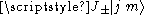is some scalarScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
multiplied by
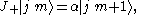
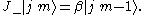
,This illustrates the defining feature of ladder operators in quantum mechanics: the incrementing (or decrementing) of a quantum number, thus mapping one quantum state onto another. This is the reason that they are often known as raising and lowering operators.
To obtain the values of α and β we first take the norm of each operator, recognizing that J+ and J- are a Hermitian conjugate pair (
),,.The product of the ladder operators can be expressed in terms of the commuting pair J2 and Jz,
Thus we can express the values of |α|2 and |β|2 in terms of the eigenvalues of J2 and Jz,
The phases
Phase factor
For any complex number written in polar form , the phase factor is the exponential part, i.e. eiθ. As such, the term "phase factor" is similar to the term phasor, although the former term is more common in quantum mechanics. This phase factor is itself a complex number of absolute value 1...
of α and β are not physically significant, thus they can be chosen to be real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and we have:
Confirming that m is bounded by the value of j (
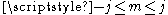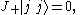
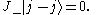
) we have:Applications in atomic and molecular physics
Many terms in the Hamiltonians of atomic or molecular systems involve the scalar product of angular momentum operators. An example is the magnetic dipole term in the hyperfine Hamiltonian,Angular momentum algebra can often be simplified by recasting it in the spherical basis. Using the notation of spherical tensor operators, the "-1", "0" and "+1" components of J(1) ≡ J are given by,
From these definitions it can be shown that the above scalar product can be expanded as
The significance of this expansion is that it clearly indicates which states are coupled by this term in the Hamiltonian, that is those with quantum numbers differing by mi = ±1 and mj = 1 only.
See also
- Creation and Annihilation OperatorsCreation and annihilation operatorsCreation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
- Quantum Harmonic OscillatorQuantum harmonic oscillatorThe quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...