Lambdavacuum solution
Encyclopedia
In general relativity
, a lambdavacuum solution is an exact solution
to the Einstein field equation in which the only term in the stress-energy tensor
is a cosmological constant
term. This can be interpreted physically as a kind of classical approximation to a nonzero vacuum energy
.
Terminological note: this article concerns a standard concept, but there is apparently no standard term to denote this concept, so we have attempted to supply one for the benefit of Wikipedia
.
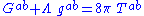
However, it is more sensible to move the extra term to the right hand side and absorb it into the stress-energy tensor
, so that the cosmological constant term becomes just another contribution to the stress-energy tensor. When other contributions vanish,
we have a lambdavacuum. Equivalently, we can write this, in terms of the Ricci tensor, in the form
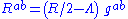
. There are two cases:
The idea of the vacuum having an energy density might seem outrageous, but this does make sense in quantum field theory. Indeed, nonzero vacuum energies can even be experimentally verified in the Casimir effect
.
rather than the coordinate basis are often called physical components, because these are the components which can (in principle) be measured by an observer. A frame consists of four unit vector fields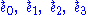
Here, the first is a timelike unit vector field and the others are spacelike unit vector fields, and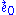
is everywhere orthogonal to the world lines of a family of observers (not necessarily inertial observers).
Remarkably, in the case of lambdavacuum, all observers measure the same energy density and the same (isotropic) pressure. That is, the Einstein tensor takes the form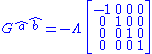
Saying that this tensor takes the same form for all observers is the same as saying that the isotropy group of a lambdavacuum is SO(1,3), the full Lorentz group
.
of the Einstein tensor of a lambdavacuum must have the form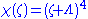
Using Newton's identities
, this condition can be re-expressed in terms of the trace
s of the powers of the Einstein tensor as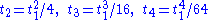
where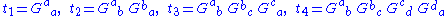
are the traces of the powers of the linear operator corresponding to the Einstein tensor, which has second rank.
Einstein manifold
s are Riemannian manifold
s in which the Ricci tensor is proportional (by some constant, not otherwise specified) to the metric tensor
. Such manifolds may have the wrong signature to admit a spacetime interpretation in general relativity, and may have the wrong dimension as well. But the Lorentzian manifolds which are also Einstein manifolds are precisely the Lambdavacuum solutions.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, a lambdavacuum solution is an exact solution
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
to the Einstein field equation in which the only term in the stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
is a cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
term. This can be interpreted physically as a kind of classical approximation to a nonzero vacuum energy
Vacuum energy
Vacuum energy is an underlying background energy that exists in space even when the space is devoid of matter . The concept of vacuum energy has been deduced from the concept of virtual particles, which is itself derived from the energy-time uncertainty principle...
.
Terminological note: this article concerns a standard concept, but there is apparently no standard term to denote this concept, so we have attempted to supply one for the benefit of Wikipedia
Wikipedia
Wikipedia is a free, web-based, collaborative, multilingual encyclopedia project supported by the non-profit Wikimedia Foundation. Its 20 million articles have been written collaboratively by volunteers around the world. Almost all of its articles can be edited by anyone with access to the site,...
.
Mathematical definition
The Einstein field equation is often written, with a so-called cosmological constant term, as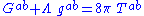However, it is more sensible to move the extra term to the right hand side and absorb it into the stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
, so that the cosmological constant term becomes just another contribution to the stress-energy tensor. When other contributions vanish,
we have a lambdavacuum. Equivalently, we can write this, in terms of the Ricci tensor, in the form
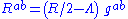
Physical interpretation
A nonzero cosmological constant term can be interpreted in terms of a nonzero vacuum energyVacuum energy
Vacuum energy is an underlying background energy that exists in space even when the space is devoid of matter . The concept of vacuum energy has been deduced from the concept of virtual particles, which is itself derived from the energy-time uncertainty principle...
. There are two cases:
: positive vacuum energy density and negative vacuum pressure (isotropic suction), as in de Sitter spaceDe Sitter spaceIn mathematics and physics, a de Sitter space is the analog in Minkowski space, or spacetime, of a sphere in ordinary, Euclidean space. The n-dimensional de Sitter space , denoted dS_n, is the Lorentzian manifold analog of an n-sphere ; it is maximally symmetric, has constant positive curvature,...
,
: negative vacuum energy density and positive vacuum pressure, as in anti-de Sitter space.
The idea of the vacuum having an energy density might seem outrageous, but this does make sense in quantum field theory. Indeed, nonzero vacuum energies can even be experimentally verified in the Casimir effect
Casimir effect
In quantum field theory, the Casimir effect and the Casimir–Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, like capacitors placed a few micrometers apart, without any external electromagnetic field...
.
Einstein tensor
The components of a tensor computed with respect to a frame fieldFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
rather than the coordinate basis are often called physical components, because these are the components which can (in principle) be measured by an observer. A frame consists of four unit vector fields
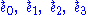
Here, the first is a timelike unit vector field and the others are spacelike unit vector fields, and
is everywhere orthogonal to the world lines of a family of observers (not necessarily inertial observers).Remarkably, in the case of lambdavacuum, all observers measure the same energy density and the same (isotropic) pressure. That is, the Einstein tensor takes the form
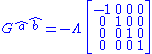
Saying that this tensor takes the same form for all observers is the same as saying that the isotropy group of a lambdavacuum is SO(1,3), the full Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
.
Eigenvalues
The characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Einstein tensor of a lambdavacuum must have the form
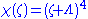
Using Newton's identities
Newton's identities
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
, this condition can be re-expressed in terms of the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
s of the powers of the Einstein tensor as
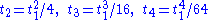
where
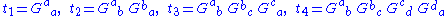
are the traces of the powers of the linear operator corresponding to the Einstein tensor, which has second rank.
Relation with Einstein manifolds
The definition of a lambdavacuum solution makes mathematical sense irrespective of any physical interpretation, and lambdavacuums are in fact a special case of a concept which is studied by pure mathematicians.Einstein manifold
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
s are Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s in which the Ricci tensor is proportional (by some constant, not otherwise specified) to the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. Such manifolds may have the wrong signature to admit a spacetime interpretation in general relativity, and may have the wrong dimension as well. But the Lorentzian manifolds which are also Einstein manifolds are precisely the Lambdavacuum solutions.
Examples
Noteworthy individual examples of lambdavacuum solutions include:- de Sitter lambdavacuumDe Sitter spaceIn mathematics and physics, a de Sitter space is the analog in Minkowski space, or spacetime, of a sphere in ordinary, Euclidean space. The n-dimensional de Sitter space , denoted dS_n, is the Lorentzian manifold analog of an n-sphere ; it is maximally symmetric, has constant positive curvature,...
, often referred to as the dS cosmological model, - anti-de Sitter lambdavacuum, often referred to as the AdS cosmological model,
- Schwarzschild–dS lambdavacuum, which models a spherically symmetric massive object immersed in a de Sitter universe (and likewise for AdS),
- Kerr–dS lambdvacuum, the rotating generalization of the latter,
- Nariai lambdavacuum; this is the only solution in general relativity, other than the Bertotti–Robinson electrovacuum, which has a Cartesian product structure.