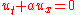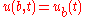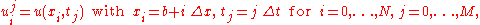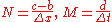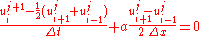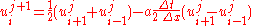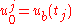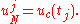Lax–Friedrichs method
Encyclopedia
The Lax–Friedrichs method, named after Peter Lax
and Kurt O. Friedrichs
, is a numerical
method for the solution of hyperbolic partial differential equation
s based on finite difference
s. The method can be described as the FTCS (forward in time, centered in space) scheme
with an artificial viscosity term of 1/2.
of the form:
on the domain
with initial condition
and the boundary conditions
If one discretizes the domain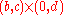
to a grid with equally spaced points with a spacing of 
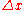in the 
-direction and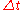 
in the 
-direction, we define
where
are integers representing the number of grid intervals. Then the Lax–Friedrichs method for solving the above partial differential equation is given by:
Or, rewriting this to solve for the unknown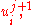
Where the initial values and boundary nodes are taken from
accurate in space and time provided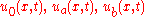
are fourth-order continuous function
s. Under these conditions, the method is stable
if and only if the following condition, derived from von Neumann stability analysis
, is satisfied:
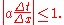
The Lax–Friedrichs method is classified as having second-order dissipation
and third order dispersion
. For functions that have discontinuities, the scheme displays strong dissipation and dispersion ; see figures at right.
Peter Lax
Peter David Lax is a mathematician working in the areas of pure and applied mathematics. He has made important contributions to integrable systems, fluid dynamics and shock waves, solitonic physics, hyperbolic conservation laws, and mathematical and scientific computing, among other fields...
and Kurt O. Friedrichs
Kurt O. Friedrichs
Kurt Otto Friedrichs was a noted German American mathematician. He was the co-founder of the Courant Institute at New York University and recipient of the National Medal of Science.-Biography:...
, is a numerical
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
method for the solution of hyperbolic partial differential equation
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
s based on finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
s. The method can be described as the FTCS (forward in time, centered in space) scheme
FTCS scheme
In numerical analysis, the FTCS method is a finite difference method used for numerically solving the heat equation and similar parabolic partial differential equations. It is a first-order method in time, explicit in time, and is conditionally stable...
with an artificial viscosity term of 1/2.
Illustration
Consider a one-dimensional, linear hyperbolic partial differential equation for of the form:
on the domain
with initial condition
and the boundary conditions
If one discretizes the domain
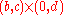to a grid with equally spaced points with a spacing of 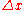in the -direction and 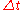in the -direction, we define
where
are integers representing the number of grid intervals. Then the Lax–Friedrichs method for solving the above partial differential equation is given by:
Or, rewriting this to solve for the unknown
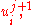
Where the initial values and boundary nodes are taken from
Stability and accuracy
This method is explicit and first orderOrders of approximation
In science, engineering, and other quantitative disciplines, orders of approximation refer to formal or informal terms for how precise an approximation is, and to indicate progressively more refined approximations: in increasing order of precision, a zeroth order approximation, a first order...
accurate in space and time provided
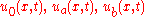are fourth-order continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s. Under these conditions, the method is stable
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
if and only if the following condition, derived from von Neumann stability analysis
Von Neumann stability analysis
In numerical analysis, von Neumann stability analysis is a procedure used to check the stability of finite difference schemes as applied to linear partial differential equations...
, is satisfied:
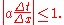
The Lax–Friedrichs method is classified as having second-order dissipation
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
and third order dispersion
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
. For functions that have discontinuities, the scheme displays strong dissipation and dispersion ; see figures at right.