
Lie point symmetry
Encyclopedia
Towards the end of the nineteenth century, Sophus Lie
introduced the notion of Lie group
in order to study the solutions of ordinary differential equations (ODEs). He showed the following main property: the order of an ordinary differential equation can be reduced by one if it is invariant
under one-parameter Lie group of point transformations. This observation unified and extended the available integration techniques. Lie devoted the remainder of his mathematical career to developing these continuous groups that have now an impact on many areas of mathematically-based sciences. The applications of Lie groups to differential systems were mainly established by Lie and Emmy Noether
, and then advocated by Élie Cartan
.
Roughly speaking, a Lie point symmetry of a system is a local group of transformations that maps every solution of the system to another solution of the same system. In other words, it maps the solution set of the system to itself. Elementary examples of Lie groups are translations
, rotations and scalings
.
The Lie symmetry theory is a well-known subject. In it are discussed continuous symmetries
opposed to, for example, discrete symmetries
. The literature for this theory can be found, among other places, in these notes..
s (dependent variables) and derivatives of the state variables up to any finite order. There are many other kinds of symmetries. For example, contact transformations
let coefficients of the transformations infinitesimal generator depend also on first derivatives of the coordinates. Lie-Bäcklund transformations let them involve derivatives up to an arbitrary order. The possibility of the existence of such symmetries was recognized by Noether. For Lie point symmetries, the coefficients of the infinitesimal generators depend only on coordinates, denoted by .
.
. In the literature, one can find the classical reduction process, and the moving frame
-based reduction process. Also symmetry groups can be used for classifying different symmetry classes of solutions.
s. These mathematical objects form a Lie algebra
of infinitesimal generators. Deduced "infinitesimal symmetry conditions" (defining equations of the symmetry group) can be explicitly solved in order to find the closed form of symmetry groups, and thus the associated infinitesimal generators.
Let be the set of coordinates on which a system is defined where
be the set of coordinates on which a system is defined where  is the cardinal of
is the cardinal of  . An infinitesimal generator
. An infinitesimal generator 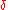 in the field
in the field  is a linear operator
is a linear operator  that has
that has  in its kernel and that satisfies the Leibniz rule
in its kernel and that satisfies the Leibniz rule
: .
.
In the canonical basis of elementary derivations , it is written as:
, it is written as:
where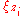 is in
is in  for all
for all  in
in  .
.
s can be generated by a generating set of infinitesimal generator
s. To every Lie group, one can associate a Lie algebra. Roughly, a Lie algebra is an algebra
is an algebra
constituted by a vector space equipped with Lie bracket
as additional operation. The base field of a Lie algebra depends on the concept of invariant
. Here only finite-dimensional Lie algebras are considered.
(or flow
) is a one-parameter group action
. Let us denote by such a dynamical system, more precisely, a (left-)action of a group
such a dynamical system, more precisely, a (left-)action of a group 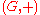 on a manifold
on a manifold
 :
:
such that for all point in
in  :
:
A continuous dynamical system is defined on a group that can be identified to
that can be identified to  i.e. the group elements are continuous.
i.e. the group elements are continuous.
, roughly speaking, is an element that does not change under a transformation.
A symmetry group of a system is a continuous dynamical system defined on a local Lie group acting on a manifold
acting on a manifold  . For the sake of clarity, we restrict ourselves to n-dimensional real manifolds
. For the sake of clarity, we restrict ourselves to n-dimensional real manifolds  where
where  is the number of system coordinates.
is the number of system coordinates.
 be a finite set of rational functions over the field
be a finite set of rational functions over the field  where
where  and
and  are polynomials in
are polynomials in  i.e. in variables
i.e. in variables  with coefficients in
with coefficients in  . An algebraic system associated to
. An algebraic system associated to  is defined by the following equalities and inequalities:
is defined by the following equalities and inequalities: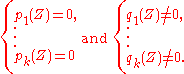
An algebraic system defined by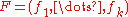 is regular (a.k.a. smooth
is regular (a.k.a. smooth
) if the system is of maximal rank
is of maximal rank  , meaning that the Jacobian matrix
, meaning that the Jacobian matrix 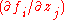 is of rank
is of rank  at every solution
at every solution  of the associated semi-algebraic variety
of the associated semi-algebraic variety
.
 is a symmetry group of an algebraic system.
is a symmetry group of an algebraic system.
Theorem. Let be a connected local Lie group of a continuous dynamical system acting in the n-dimensional space
be a connected local Lie group of a continuous dynamical system acting in the n-dimensional space  . Let
. Let  with
with  define a regular system of algebraic equations:
define a regular system of algebraic equations:
Then is a symmetry group of this algebraic system if, and only if,
is a symmetry group of this algebraic system if, and only if,
for every infinitesimal generator in the Lie algebra
in the Lie algebra  of
of  .
.
 with:
with:
The infinitesimal generator
is associated to one of the one-parameter symmetry groups. It acts on 4 variables, namely and
and  . One can easily verify that
. One can easily verify that  and
and  . Thus the relations
. Thus the relations  are satisfied for any
are satisfied for any  in
in  that vanishes the algebraic system.
that vanishes the algebraic system.
 be a derivation w.r.t. the continuous independent variable
be a derivation w.r.t. the continuous independent variable  . We consider two sets
. We consider two sets  and
and  . The associated coordinate set is defined by
. The associated coordinate set is defined by  and its cardinal is
and its cardinal is  . With these notations, a system of first-order ODEs is a system where:
. With these notations, a system of first-order ODEs is a system where:
and the set specifies the evolution of state variables of ODEs w.r.t. the independent variable. The elements of the set
specifies the evolution of state variables of ODEs w.r.t. the independent variable. The elements of the set  are called state variables, these of
are called state variables, these of  parameters.
parameters.
One can associate also a continuous dynamical system to a system of ODEs by resolving its equations.
An infinitesimal generator is a derivation that is closely related to systems of ODEs (more precisely to continuous dynamical systems). For the link between a system of ODEs, the associated vector field and the infinitesimal generator, see section 1.3 of. The infinitesimal generator associated to a system of ODEs, described as above, is defined with the same notations as follows:
associated to a system of ODEs, described as above, is defined with the same notations as follows:
 be a continuous dynamical system and
be a continuous dynamical system and  its infinitesimal generator. A continuous dynamical system
its infinitesimal generator. A continuous dynamical system  is a Lie point symmetry of
is a Lie point symmetry of  if, and only if,
if, and only if,  sends every orbit of
sends every orbit of  to an orbit. Hence, the infinitesimal generator
to an orbit. Hence, the infinitesimal generator  satisfies the following relation based on Lie bracket
satisfies the following relation based on Lie bracket
:
where is any constant of
is any constant of  and
and  i.e.
i.e.  . These generators are linearly independent.
. These generators are linearly independent.
One does not need the explicit formulas of in order to compute the infinitesimal generators of its symmetries.
in order to compute the infinitesimal generators of its symmetries.
's logistic growth model with linear predation, where the state variable represents a population. The parameter
represents a population. The parameter  is the difference between the growth and predation rate and the parameter
is the difference between the growth and predation rate and the parameter  corresponds to the receptive capacity of the environment:
corresponds to the receptive capacity of the environment:
The continuous dynamical system associated to this system of ODEs is:
The independent variable varies continuously; thus the associated group can be identified with
varies continuously; thus the associated group can be identified with  .
.
The infinitesimal generator associated to this system of ODEs is:
The following infinitesimal generators belong to the 2-dimensional symmetry group of :
:
provides some Lie symmetry methods for PDEs
. It manipulates integration of determining systems and also differential form
s. Despite its success on small systems, its integration capabilities for solving determining systems automatically are limited by complexity issues. The DETools package uses the prolongation of vector field
s for searching Lie symmetries of ODEs. Finding Lie symmetries for ODEs, in the general case, may be as complicated as solving the original system.
Sophus Lie
Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
introduced the notion of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
in order to study the solutions of ordinary differential equations (ODEs). He showed the following main property: the order of an ordinary differential equation can be reduced by one if it is invariant
Invariant
Invariant and invariance may have several meanings, among which are:- Computer science :* Invariant , an Expression whose value doesn't change during program execution* A type in overriding that is neither covariant nor contravariant...
under one-parameter Lie group of point transformations. This observation unified and extended the available integration techniques. Lie devoted the remainder of his mathematical career to developing these continuous groups that have now an impact on many areas of mathematically-based sciences. The applications of Lie groups to differential systems were mainly established by Lie and Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
, and then advocated by Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
.
Roughly speaking, a Lie point symmetry of a system is a local group of transformations that maps every solution of the system to another solution of the same system. In other words, it maps the solution set of the system to itself. Elementary examples of Lie groups are translations
Translations
Translations is a three-act play by Irish playwright Brian Friel written in 1980. It is set in Baile Beag , a small village at the heart of 19th century agricultural Ireland...
, rotations and scalings
Scaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
.
The Lie symmetry theory is a well-known subject. In it are discussed continuous symmetries
Continuous symmetry
In mathematics, continuous symmetry is an intuitive idea corresponding to the concept of viewing some symmetries as motions, as opposed to e.g. reflection symmetry, which is invariance under a kind of flip from one state to another. It has largely and successfully been formalised in the...
opposed to, for example, discrete symmetries
Discrete symmetry
A discrete symmetry is a symmetry that describes non-continuous changes in a system. For example, a square possesses discrete rotational symmetry, as only rotations by multiples of right angles will preserve the square's original appearance. Discrete symmetries sometimes involve some type of...
. The literature for this theory can be found, among other places, in these notes..
Types of symmetries
Lie groups and hence their infinitesimal generators can be naturally "extended" to act on the space of independent variables, state variableState variable
A state variable is one of the set of variables that describe the "state" of a dynamical system. Intuitively, the state of a system describes enough about the system to determine its future behaviour...
s (dependent variables) and derivatives of the state variables up to any finite order. There are many other kinds of symmetries. For example, contact transformations
Contact geometry
In mathematics, contact geometry is the study of a geometric structure on smooth manifolds given by a hyperplane distribution in the tangent bundle and specified by a one-form, both of which satisfy a 'maximum non-degeneracy' condition called 'complete non-integrability'...
let coefficients of the transformations infinitesimal generator depend also on first derivatives of the coordinates. Lie-Bäcklund transformations let them involve derivatives up to an arbitrary order. The possibility of the existence of such symmetries was recognized by Noether. For Lie point symmetries, the coefficients of the infinitesimal generators depend only on coordinates, denoted by
 .
.Applications
Lie symmetries were introduced by Lie in order to solve ordinary differential equations. Another application of symmetry methods is to reduce systems of differential equations, finding equivalent systems of differential equations of simpler form. This is called reductionReduction (mathematics)
In mathematics, reduction refers to the rewriting of an expression into a simpler form. For example, the process of rewriting a fraction into one with the smallest whole-number denominator possible is called "reducing a fraction"...
. In the literature, one can find the classical reduction process, and the moving frame
Moving frame
In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
-based reduction process. Also symmetry groups can be used for classifying different symmetry classes of solutions.
Infinitesimal approach
Lie's fundamental theorems underline that Lie groups can be characterized by their infinitesimal generatorInfinitesimal generator
In mathematics, the term infinitesimal generator may refer to:* an element of the Lie algebra associated to a Lie group;* the infinitesimal generator of a stochastic process;* the infinitesimal generator of a strongly continuous semigroup....
s. These mathematical objects form a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of infinitesimal generators. Deduced "infinitesimal symmetry conditions" (defining equations of the symmetry group) can be explicitly solved in order to find the closed form of symmetry groups, and thus the associated infinitesimal generators.
Let
 be the set of coordinates on which a system is defined where
be the set of coordinates on which a system is defined where  is the cardinal of
is the cardinal of  . An infinitesimal generator
. An infinitesimal generator 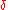 in the field
in the field  is a linear operator
is a linear operator  that has
that has  in its kernel and that satisfies the Leibniz rule
in its kernel and that satisfies the Leibniz ruleProduct rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
:
 .
.In the canonical basis of elementary derivations
 , it is written as:
, it is written as:
where
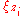 is in
is in  for all
for all  in
in  .
.Lie groups and Lie algebras of infinitesimal generators
Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s can be generated by a generating set of infinitesimal generator
Infinitesimal generator
In mathematics, the term infinitesimal generator may refer to:* an element of the Lie algebra associated to a Lie group;* the infinitesimal generator of a stochastic process;* the infinitesimal generator of a strongly continuous semigroup....
s. To every Lie group, one can associate a Lie algebra. Roughly, a Lie algebra
 is an algebra
is an algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
constituted by a vector space equipped with Lie bracket
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
as additional operation. The base field of a Lie algebra depends on the concept of invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
. Here only finite-dimensional Lie algebras are considered.
Continuous dynamical systems
A dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
(or flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
) is a one-parameter group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. Let us denote by
 such a dynamical system, more precisely, a (left-)action of a group
such a dynamical system, more precisely, a (left-)action of a group 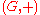 on a manifold
on a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
 :
:
such that for all point
 in
in  :
:
-
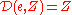 where
where  is the neutral element of
is the neutral element of  ;
; - for all
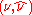 in
in 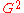 ,
,  .
.
A continuous dynamical system is defined on a group
 that can be identified to
that can be identified to  i.e. the group elements are continuous.
i.e. the group elements are continuous.Invariants
An invariantInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
, roughly speaking, is an element that does not change under a transformation.
Definition of Lie point symmetries
In this paragraph, we consider precisely expanded Lie point symmetries i.e. we work in an expanded space meaning that the distinction between independent variable, state variables and parameters are avoided as much as possible.A symmetry group of a system is a continuous dynamical system defined on a local Lie group
 acting on a manifold
acting on a manifold  . For the sake of clarity, we restrict ourselves to n-dimensional real manifolds
. For the sake of clarity, we restrict ourselves to n-dimensional real manifolds  where
where  is the number of system coordinates.
is the number of system coordinates.Lie point symmetries of algebraic systems
Let us define algebraic systems used in the forthcoming symmetry definition.Algebraic systems
Let be a finite set of rational functions over the field
be a finite set of rational functions over the field  where
where  and
and  are polynomials in
are polynomials in  i.e. in variables
i.e. in variables  with coefficients in
with coefficients in  . An algebraic system associated to
. An algebraic system associated to  is defined by the following equalities and inequalities:
is defined by the following equalities and inequalities: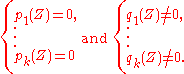
An algebraic system defined by
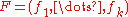 is regular (a.k.a. smooth
is regular (a.k.a. smoothSmooth
Smooth means having a texture that lacks friction. Not rough.Smooth may also refer to:-In mathematics:* Smooth function, a function that is infinitely differentiable; used in calculus and topology...
) if the system
 is of maximal rank
is of maximal rank  , meaning that the Jacobian matrix
, meaning that the Jacobian matrix 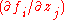 is of rank
is of rank  at every solution
at every solution  of the associated semi-algebraic variety
of the associated semi-algebraic varietyAlgebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
.
Definition of Lie point symmetries
The following theorem (see th. 2.8 in ch.2 of ) gives necessary and sufficient conditions so that a local Lie group is a symmetry group of an algebraic system.
is a symmetry group of an algebraic system.Theorem. Let
 be a connected local Lie group of a continuous dynamical system acting in the n-dimensional space
be a connected local Lie group of a continuous dynamical system acting in the n-dimensional space  . Let
. Let  with
with  define a regular system of algebraic equations:
define a regular system of algebraic equations:
Then
 is a symmetry group of this algebraic system if, and only if,
is a symmetry group of this algebraic system if, and only if,
for every infinitesimal generator
 in the Lie algebra
in the Lie algebra  of
of  .
.Example
Let us consider the algebraic system defined on a space of 6 variables, namely with:
with:
The infinitesimal generator

is associated to one of the one-parameter symmetry groups. It acts on 4 variables, namely
 and
and  . One can easily verify that
. One can easily verify that  and
and  . Thus the relations
. Thus the relations  are satisfied for any
are satisfied for any  in
in  that vanishes the algebraic system.
that vanishes the algebraic system.Lie point symmetries of dynamical systems
Let us define systems of first-order ODEs used in the forthcoming symmetry definition.Systems of ODEs and associated infinitesimal generators
Let be a derivation w.r.t. the continuous independent variable
be a derivation w.r.t. the continuous independent variable  . We consider two sets
. We consider two sets  and
and  . The associated coordinate set is defined by
. The associated coordinate set is defined by  and its cardinal is
and its cardinal is  . With these notations, a system of first-order ODEs is a system where:
. With these notations, a system of first-order ODEs is a system where:
and the set
 specifies the evolution of state variables of ODEs w.r.t. the independent variable. The elements of the set
specifies the evolution of state variables of ODEs w.r.t. the independent variable. The elements of the set  are called state variables, these of
are called state variables, these of  parameters.
parameters.One can associate also a continuous dynamical system to a system of ODEs by resolving its equations.
An infinitesimal generator is a derivation that is closely related to systems of ODEs (more precisely to continuous dynamical systems). For the link between a system of ODEs, the associated vector field and the infinitesimal generator, see section 1.3 of. The infinitesimal generator
 associated to a system of ODEs, described as above, is defined with the same notations as follows:
associated to a system of ODEs, described as above, is defined with the same notations as follows:
Definition of Lie point symmetries
Here is a geometrical definition of such symmetries. Let be a continuous dynamical system and
be a continuous dynamical system and  its infinitesimal generator. A continuous dynamical system
its infinitesimal generator. A continuous dynamical system  is a Lie point symmetry of
is a Lie point symmetry of  if, and only if,
if, and only if,  sends every orbit of
sends every orbit of  to an orbit. Hence, the infinitesimal generator
to an orbit. Hence, the infinitesimal generator  satisfies the following relation based on Lie bracket
satisfies the following relation based on Lie bracketLie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
:

where
 is any constant of
is any constant of  and
and  i.e.
i.e.  . These generators are linearly independent.
. These generators are linearly independent.One does not need the explicit formulas of
 in order to compute the infinitesimal generators of its symmetries.
in order to compute the infinitesimal generators of its symmetries.Example
Consider Pierre François VerhulstPierre François Verhulst
Pierre François Verhulst was a mathematician and a doctor in number theory from the University of Ghent in 1825...
's logistic growth model with linear predation, where the state variable
 represents a population. The parameter
represents a population. The parameter  is the difference between the growth and predation rate and the parameter
is the difference between the growth and predation rate and the parameter  corresponds to the receptive capacity of the environment:
corresponds to the receptive capacity of the environment:
The continuous dynamical system associated to this system of ODEs is:

The independent variable
 varies continuously; thus the associated group can be identified with
varies continuously; thus the associated group can be identified with  .
.The infinitesimal generator associated to this system of ODEs is:

The following infinitesimal generators belong to the 2-dimensional symmetry group of
 :
:
Software
There exist many software packages in this area. For example, the package liesymm of MapleMaple (software)
Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....
provides some Lie symmetry methods for PDEs
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
. It manipulates integration of determining systems and also differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s. Despite its success on small systems, its integration capabilities for solving determining systems automatically are limited by complexity issues. The DETools package uses the prolongation of vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s for searching Lie symmetries of ODEs. Finding Lie symmetries for ODEs, in the general case, may be as complicated as solving the original system.

