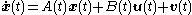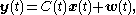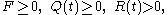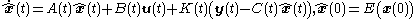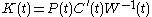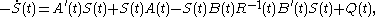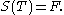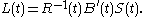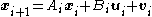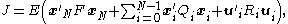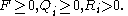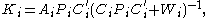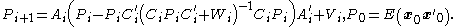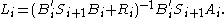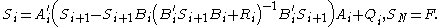Linear-quadratic-Gaussian control
Encyclopedia
In control theory
, the linear-quadratic-Gaussian (LQG) control problem is one of the most fundamental optimal control
problems. It concerns uncertain linear system
s disturbed by additive white Gaussian noise
, having incomplete state information (i.e. not all the state variables are measured and available for feedback) and undergoing control subject to quadratic costs. Moreover the solution is unique and constitutes a linear dynamic feedback control law that is easily computed and implemented. Finally the LQG controller is also fundamental to the optimal perturbation control of non-linear systems.
The LQG controller is simply the combination of a Kalman filter
i.e. a linear-quadratic estimator (LQE) with a linear-quadratic regulator
(LQR). The separation principle
guarantees that these can be designed and computed independently. LQG control applies to both linear time-invariant systems as well as linear time-varying systems. The application to linear time-invariant systems is well known. The application to linear time-varying system
s enables the design of linear feedback controllers for non-linear uncertain systems.
The LQG controller itself is a dynamic system like the system it controls. Both systems have the same state dimension. Therefore implementing the LQG controller may be problematic if the dimension of the system state is large. The reduced-order LQG problem (fixed-order LQG problem) overcomes this by fixing a-priori the number of states of the LQG controller. This problem is more difficult to solve because it is no longer separable. Also the solution is no longer unique. Despite these facts numerical algorithms are available to solve the associated optimal projection equations
which constitute necessary and sufficient conditions for a locally optimal reduced-order LQG controller.
Finally, a word of caution. LQG optimality does not automatically ensure good robustness properties. The robust stability of the closed loop system must be checked separately after the LQG controller has been designed. To promote robustness some of the system parameters may be assumed stochastic instead of deterministic. The associated more difficult control problem leads to a similar optimal controller of which only the controller parameters are different.
where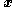
represents the vector of state variables of the system, 
the vector of control inputs and 
the vector of measured outputs available for feedback. Both additive white Gaussian system noise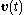 
and additive white Gaussian measurement noise 
affect the system. Given this system the objective is to find the control input history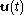 
which at every time 
may depend only on the past measurements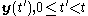 
such that the following cost function is minimized,
where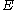
denotes the expected value
. The final time (horizon)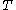
may be either finite or infinite. If the horizon tends to infinity the first term 
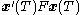of the cost function becomes negligible and irrelevant to the problem. Also to keep the costs finite the cost function has to be taken to be 
.
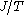The LQG controller that solves the LQG control problem is specified by the following equations,
The matrix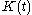
is called the Kalman gain of the associated Kalman filter
represented by the first equation. At each time
this filter generates estimates 
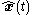of the state 
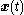using the past measurements and inputs. The Kalman gain 
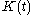is computed from the matrices 
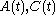, the two intensity matrices 
, 
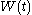associated to the white Gaussian noises 
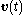and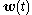 
and finally 
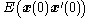. These five matrices determine the Kalman gain through the following associated matrix Riccati differential equation,
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, the linear-quadratic-Gaussian (LQG) control problem is one of the most fundamental optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
problems. It concerns uncertain linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
s disturbed by additive white Gaussian noise
Additive white Gaussian noise
Additive white Gaussian noise is a channel model in which the only impairment to communication is a linear addition of wideband or white noise with a constant spectral density and a Gaussian distribution of amplitude. The model does not account for fading, frequency selectivity, interference,...
, having incomplete state information (i.e. not all the state variables are measured and available for feedback) and undergoing control subject to quadratic costs. Moreover the solution is unique and constitutes a linear dynamic feedback control law that is easily computed and implemented. Finally the LQG controller is also fundamental to the optimal perturbation control of non-linear systems.
The LQG controller is simply the combination of a Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
i.e. a linear-quadratic estimator (LQE) with a linear-quadratic regulator
Linear-quadratic regulator
The theory of optimal control is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equations and the cost is described by a quadratic functional is called the LQ problem...
(LQR). The separation principle
Separation principle
In control theory, a separation principle, more formally known as a principle of separation of estimation and control, states that under some assumptions the problem of designing an optimal feedback controller for a stochastic system can be solved by designing an optimal observer for the state of...
guarantees that these can be designed and computed independently. LQG control applies to both linear time-invariant systems as well as linear time-varying systems. The application to linear time-invariant systems is well known. The application to linear time-varying system
Time-variant system
A time-variant system is a system that is not time invariant . Roughly speaking, characteristics of its output depend explicitly upon time.- Overview :...
s enables the design of linear feedback controllers for non-linear uncertain systems.
The LQG controller itself is a dynamic system like the system it controls. Both systems have the same state dimension. Therefore implementing the LQG controller may be problematic if the dimension of the system state is large. The reduced-order LQG problem (fixed-order LQG problem) overcomes this by fixing a-priori the number of states of the LQG controller. This problem is more difficult to solve because it is no longer separable. Also the solution is no longer unique. Despite these facts numerical algorithms are available to solve the associated optimal projection equations
Optimal projection equations
In control, the Linear-Quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, incomplete state information also disturbed by additive white Gaussian noise and quadratic costs...
which constitute necessary and sufficient conditions for a locally optimal reduced-order LQG controller.
Finally, a word of caution. LQG optimality does not automatically ensure good robustness properties. The robust stability of the closed loop system must be checked separately after the LQG controller has been designed. To promote robustness some of the system parameters may be assumed stochastic instead of deterministic. The associated more difficult control problem leads to a similar optimal controller of which only the controller parameters are different.
Continuous time
Consider the linear dynamic system,
where
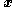represents the vector of state variables of the system, the vector of control inputs and the vector of measured outputs available for feedback. Both additive white Gaussian system noise 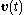and additive white Gaussian measurement noise affect the system. Given this system the objective is to find the control input history 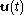which at every time may depend only on the past measurements 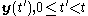such that the following cost function is minimized,
where
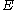denotes the expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
. The final time (horizon)
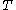may be either finite or infinite. If the horizon tends to infinity the first term 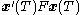of the cost function becomes negligible and irrelevant to the problem. Also to keep the costs finite the cost function has to be taken to be 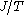.The LQG controller that solves the LQG control problem is specified by the following equations,
The matrix
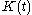is called the Kalman gain of the associated Kalman filterKalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
represented by the first equation. At each time
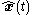this filter generates estimates of the state 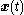using the past measurements and inputs. The Kalman gain 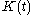is computed from the matrices 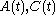, the two intensity matrices , 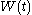associated to the white Gaussian noises 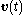and 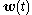and finally 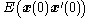. These five matrices determine the Kalman gain through the following associated matrix Riccati differential equation,-
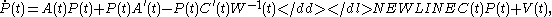
Given the solution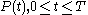
the Kalman gain equals,
The matrix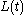
is called the feedback gain matrix. This matrix is determined by the matrices 
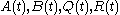and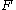 
through the following associated matrix Riccati differential equation,
Given the solution
the feedback gain equals,
Observe the similarity of the two matrix Riccati differential equations, the first one running forward in time, the second one running backward in time. This similarity is called duality. The first matrix Riccati differential equation solves the linear-quadratic estimation problem (LQE). The second matrix Riccati differential equation solves the linear-quadratic regulatorLinear-quadratic regulatorThe theory of optimal control is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equations and the cost is described by a quadratic functional is called the LQ problem...
problem (LQR). These problems are dual and together they solve the linear-quadratic-Gaussian control problem (LQG). So the LQG problem separates into the LQE and LQR problem that can be solved independently. Therefore the LQG problem is called separable.
When
and the noise intensity matrices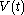 
, 
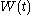do not depend on 
and when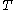 
tends to infinity the LQG controller becomes a time-invariant dynamic system. In that case both matrix Riccati differential equations may be replaced by the two associated algebraic Riccati equationAlgebraic Riccati equationThe algebraic Riccati equation is either of the following matrix equations:the continuous time algebraic Riccati equation :or the discrete time algebraic Riccati equation :...
s.
Discrete time
Since the discrete-time LQG control problem is similar to the one in continuous-time the description below focuses on the mathematical equations.
Discrete-time linear system equations:
Here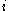
represents the discrete time index and 
represent discrete-time Gaussian white noise processes with covariance matrices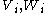 
respectively.
The quadratic cost function to be minimized:
The discrete-time LQG controller:
,
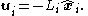
The Kalman gain equals,
where
is determined by the following matrix Riccati difference equation that runs forward in time,
The feedback gain matrix equals,
where
is determined by the following matrix Riccati difference equation that runs backward in time,
If all the matrices in the problem formulation are time-invariant and if the horizon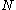
tends to infinity the discrete-time LQG controller becomes time-invariant. In that case the matrix Riccati difference equations may be replaced by their associated discrete-time algebraic Riccati equationAlgebraic Riccati equationThe algebraic Riccati equation is either of the following matrix equations:the continuous time algebraic Riccati equation :or the discrete time algebraic Riccati equation :...
s. These determine the time-invarant linear-quadratic estimator and the time-invariant linear-quadratic regulatorLinear-quadratic regulatorThe theory of optimal control is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equations and the cost is described by a quadratic functional is called the LQ problem...
in discrete-time. To keep the costs finite instead of
one has to consider 
in this case.
-
