
Separation principle
Encyclopedia
In control theory
, a separation principle, more formally known as a principle of separation of estimation and control, states that under some assumptions the problem of designing an optimal feedback controller for a stochastic system can be solved by designing an optimal observer
for the state of the system, which feeds into an optimal deterministic controller
for the system. Thus the problem can be broken into two separate parts, which facilitates the design.
As an example of such a principle, it has been proved that if a stable
observer
and stable state feedback
are designed for a linear time-invariant system
, then the combined observer and feedback will be stable. The separation principle does not hold in general (for example for non-linear systems). Another example is the separation of the linear-quadratic-Gaussian control
solution into the Kalman filter
and optimal controller for a linear-quadratic regulator
. A separation principle also exists for the control of a quantum systems.
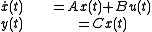
where
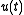 represents the input signal,
represents the input signal,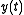 represents the output signal, and
represents the output signal, and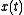 represents the internal state of the system.
represents the internal state of the system.
We can design the an observer of the form
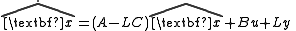
And state feedback
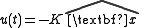
Define the error e:

Then


Now we can write the closed-loop dynamics as
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, a separation principle, more formally known as a principle of separation of estimation and control, states that under some assumptions the problem of designing an optimal feedback controller for a stochastic system can be solved by designing an optimal observer
State observer
In control theory, a state observer is a system that models a real system in order to provide an estimate of its internal state, given measurements of the input and output of the real system. It is typically a computer-implemented mathematical model....
for the state of the system, which feeds into an optimal deterministic controller
Controller (control theory)
In control theory, a controller is a device which monitors and affects the operational conditions of a given dynamical system. The operational conditions are typically referred to as output variables of the system which can be affected by adjusting certain input variables...
for the system. Thus the problem can be broken into two separate parts, which facilitates the design.
As an example of such a principle, it has been proved that if a stable
BIBO stability
In electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
observer
State observer
In control theory, a state observer is a system that models a real system in order to provide an estimate of its internal state, given measurements of the input and output of the real system. It is typically a computer-implemented mathematical model....
and stable state feedback
Feedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
are designed for a linear time-invariant system
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
, then the combined observer and feedback will be stable. The separation principle does not hold in general (for example for non-linear systems). Another example is the separation of the linear-quadratic-Gaussian control
Linear-quadratic-Gaussian control
In control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
solution into the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
and optimal controller for a linear-quadratic regulator
Linear-quadratic regulator
The theory of optimal control is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equations and the cost is described by a quadratic functional is called the LQ problem...
. A separation principle also exists for the control of a quantum systems.
Proof of separation principle for LTI systems
Consider the system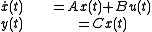
where
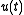 represents the input signal,
represents the input signal,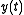 represents the output signal, and
represents the output signal, and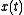 represents the internal state of the system.
represents the internal state of the system.We can design the an observer of the form
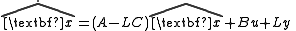
And state feedback
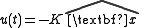
Define the error e:

Then


Now we can write the closed-loop dynamics as
-
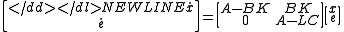
Since this is triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
, the eigenvalues are just those of A − BK together with those of A − LC. Thus the stability of the observer and feedback are independentLinear independenceIn linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
.

