Linear entropy
Encyclopedia
In quantum mechanics
, and especially quantum information theory
, the linear entropy of a state is a scalar
defined as
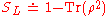
where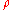
is the density matrix
of the state.
The linear entropy can range between zero, corresponding to a completely pure state, and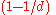
, corresponding to a completely mixed state. (Here, 
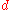is the dimension
of the density matrix.)
Linear entropy is trivially related to the purity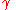
of a state by
, which is defined as
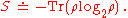
The linear entropy is obtained by approximating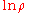
with the first order term 
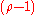in the Mercator series
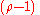
where the unit trace property of the density matrix has been used to get the second to last equality.
The linear entropy and Von Neumann entropy are similar measures of the "mixedness" of a state, although the linear entropy is easier to calculate because it does not require the diagonalization
of the density matrix.
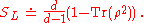
This ensures that the quantity ranges from zero to unity.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, and especially quantum information theory
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
, the linear entropy of a state is a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
defined as
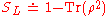
where
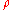is the density matrixDensity matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
of the state.
The linear entropy can range between zero, corresponding to a completely pure state, and
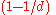, corresponding to a completely mixed state. (Here, 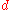is the dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of the density matrix.)
Linear entropy is trivially related to the purity
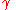of a state byMotivation
The linear entropy is an approximation to the Von Neumann entropyVon Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
, which is defined as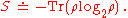The linear entropy is obtained by approximating
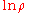with the first order term 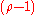in the Mercator series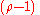where the unit trace property of the density matrix has been used to get the second to last equality.
The linear entropy and Von Neumann entropy are similar measures of the "mixedness" of a state, although the linear entropy is easier to calculate because it does not require the diagonalization
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
of the density matrix.
Alternate definition
Some authors define linear entropy with a different normalization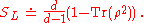This ensures that the quantity ranges from zero to unity.