
Linear flow on the torus
Encyclopedia
In mathematics
, especially in the area of mathematical analysis
known as dynamical systems theory
, a linear flow on the torus is a flow
on the n-dimensional torus
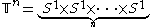
which is represented by the following differential equations with respect to the standard angular coordinates (θ1, θ2, ..., θn):
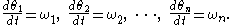
The solution of these equations can explicitly be expressed as
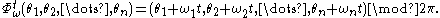
If we respesent the torus as Rn/Zn we see that a starting point is moved by the flow in the direction ω=(ω1, ω2, ..., ωn) at constant speed and when it reaches the border of the unitary n-cube it jumps to the opposite face of the cube.
For a linear flow on the torus either all orbits are periodic or all orbits are dense
on a subset of the n-torus which is a k-torus. When the components of ω are rationally independent
all the orbits are dense on the whole space. This can be easily seen in the two dimensional case: if the two components of ω are rationally independent then the Poincare section of the flow on an edge of the unit square is an irrational rotation
on a circle and therefore its orbits are dense on the circle, as a consequence the orbits of the flow must be dense on the torus.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
known as dynamical systems theory
Dynamical systems theory
Dynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
, a linear flow on the torus is a flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
on the n-dimensional torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
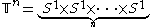
which is represented by the following differential equations with respect to the standard angular coordinates (θ1, θ2, ..., θn):
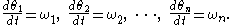
The solution of these equations can explicitly be expressed as
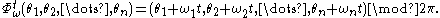
If we respesent the torus as Rn/Zn we see that a starting point is moved by the flow in the direction ω=(ω1, ω2, ..., ωn) at constant speed and when it reaches the border of the unitary n-cube it jumps to the opposite face of the cube.
For a linear flow on the torus either all orbits are periodic or all orbits are dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
on a subset of the n-torus which is a k-torus. When the components of ω are rationally independent
Rational dependence
In mathematics, a collection of real numbers is rationally independent if none of them can be written as a linear combination of the other numbers in the collection with rational coefficients. A collection of numbers which is not rationally independent is called rationally dependent...
all the orbits are dense on the whole space. This can be easily seen in the two dimensional case: if the two components of ω are rationally independent then the Poincare section of the flow on an edge of the unit square is an irrational rotation
Irrational rotation
In mathematical theory of dynamical systems, an irrational rotation is a mapwhere θ is an irrational number. Under the identification of a circle with R/Z, or with the interval [0, 1] with the boundary points glued together, this map becomes a rotation of a circle by a proportion θ of a full...
on a circle and therefore its orbits are dense on the circle, as a consequence the orbits of the flow must be dense on the torus.

