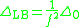Liouville's equation
Encyclopedia
- For Liouville's equation in quantum mechanics, see Density operator#Von Neumann equation.
In differential geometry, Liouville's equation, named after Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
, is the nonlinear ordinary differential equation satisfied by the conformal factor f of a metric
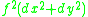 on a surface of constant Gaussian curvature
on a surface of constant Gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
K:
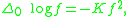
where
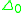 is the flat Laplace operator
is the flat Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
.

Liouville's equation typically appears in differential geometry books under the heading isothermal coordinates
Isothermal coordinates
In mathematics, specifically in differential geometry, isothermal coordinates on a Riemannian manifoldare local coordinates where the metric isconformal to the Euclidean metric...
. This term refers to the coordinates x,y, while f can be described as the conformal factor with respect to the flat metric (sometimes the square
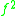 is referred to as the conformal factor, instead of f itself).
is referred to as the conformal factor, instead of f itself).Replacing f using
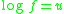 , we obtain another commonly found form of the same equation:
, we obtain another commonly found form of the same equation: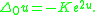
Laplace-Beltrami operator
In a more invariant fashion, the equation can be written in terms of the intrinsic Laplace-Beltrami operatorLaplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
as follows:
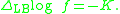
Relation to Gauss–Codazzi equations
Liouville's equation is a consequence of the Gauss–Codazzi equationsGauss–Codazzi equations
In Riemannian geometry, the Gauss–Codazzi–Mainardi equations are fundamental equations in the theory of embedded hypersurfaces in a Euclidean space, and more generally submanifolds of Riemannian manifolds...
when the metric is written in isothermal coordinates
Isothermal coordinates
In mathematics, specifically in differential geometry, isothermal coordinates on a Riemannian manifoldare local coordinates where the metric isconformal to the Euclidean metric...
.
General solution
In a simply connected domain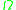 the general solution is given by
the general solution is given by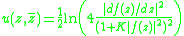
where
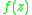 is a locally univalent meromorphic function
is a locally univalent meromorphic functionMeromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
and
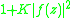 when
when 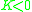 .
.