
Gauss–Codazzi equations
Encyclopedia
In Riemannian geometry
, the Gauss–Codazzi–Mainardi equations are fundamental equations in the theory of embedded hypersurface
s in a Euclidean space
, and more generally submanifold
s of Riemannian manifold
s. They also have applications for embedded hypersurfaces of pseudo-Riemannian manifold
s: see Gauss–Codazzi equations (relativity).
In the classical differential geometry of surfaces
, the Gauss–Codazzi–Mainardi equations consist of a pair of related equations. The first equation, sometimes called the Gauss equation, relates the intrinsic curvature (or Gauss curvature) of the surface to the derivatives of the Gauss map
, via the second fundamental form. This equation is the basis for Gauss's theorema egregium
. The second equation, sometimes called the Codazzi–Mainardi equation, is a structural condition on the second derivatives of the Gauss map.
It was named for Gaspare Mainardi
(1856) and Delfino Codazzi
(1868–1869), who independently derived the result , although it was discovered earlier by .
It incorporates the extrinsic curvature (or mean curvature
) of the surface. The equations show that the components of the second fundamental form and its derivatives along the surface completely classify the surface up to a Euclidean transformation, a theorem of Ossian Bonnet.
of M into that of P by the pushforward, and the cokernel
is the normal bundle
of M: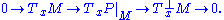
The metric splits this short exact sequence, and so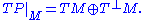
Relative to this splitting, the Levi-Civita connection
∇′ of P decomposes into tangential and normal components. For each X ∈ TM and vector field Y on M,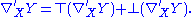
Let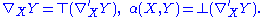
Gauss' formula now asserts that ∇X is the Levi-Civita connection for M, and α is a symmetric vector-valued form
with values in the normal bundle. It is often referred to as the second fundamental form.
An immediate corollary is the Gauss equation. For X, Y, Z, W ∈ TM,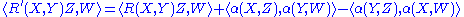
where R′ is the Riemann curvature tensor
of P and R is that of M.
The Weingarten equation is an analog of the Gauss formula for a connection in the normal bundle. Let X ∈ TM and ξ a normal vector field. Then decompose the ambient covariant derivative of ξ along X into tangential and normal components:
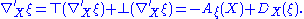
Then
There are thus a pair of connections: ∇, defined on the tangent bundle of M; and D, defined on the normal bundle of M. These combine to form a connection on any tensor product of copies of TM and T⊥M. In particular, they defined the covariant derivative of α: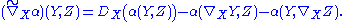
The Codazzi–Mainardi equation is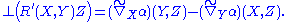
Since every immersion is, in particular, a local embedding, the above formulas also hold for immersions.
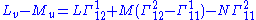
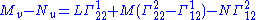
in Euclidean space,
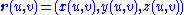
where the three component functions depend smoothly on ordered pairs (u,v) in some open domain U in the uv-plane. Assume that this surface is regular, meaning that the vectors ru and rv are linearly independent. Complete this to a basis{ru,rv,n}, by selecting a unit vector n normal to the surface. It is possible to express the second partial derivatives of r using the Christoffel symbols
and the second fundamental form.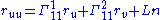
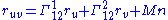
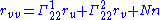
Clairaut's theorem states that partial derivatives commute: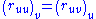
If we differentiate ruu with respect to v and ruv with respect to u, we get:
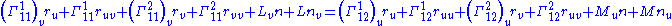
Now substitute the above expressions for the second derivatives and equate the coefficients of n: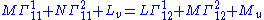
Rearranging this equation gives the first Codazzi–Mainardi equation.
The second equation may be derived similarly.
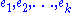 be a local orthonormal frame of vector fields normal to M. Then we can write,
be a local orthonormal frame of vector fields normal to M. Then we can write,
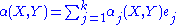
If, now,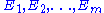 is a local orthonormal frame (of tangent vector fields) on the same open subset of M, then we can define the mean curvature
is a local orthonormal frame (of tangent vector fields) on the same open subset of M, then we can define the mean curvature
s of the immersion by
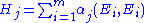
In particular, if M is a hypersurface of P, i.e. , then there is only one mean curvature to speak of. The immersion is called minimal
, then there is only one mean curvature to speak of. The immersion is called minimal
if all the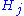 are identically zero.
are identically zero.
Observe that the mean curvature is a trace, or average, of the second fundamental form, for any given component. Sometimes mean curvature is defined by multiplying the sum on the right-hand side by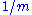 .
.
We can now write the Gauss–Codazzi equations as
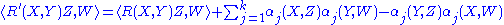
Contracting the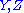 components gives us
components gives us
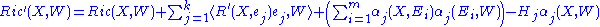
Observe that the tensor in parentheses is symmetric and nonnegative-definite in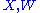 . Assuming that M is a hypersurface, this simplifies to
. Assuming that M is a hypersurface, this simplifies to
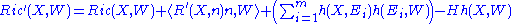
where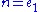 and
and 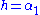 and
and 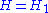 . In that case, one more contraction yields,
. In that case, one more contraction yields,
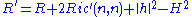
where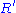 and
and 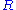 are the respective scalar curvatures, and
are the respective scalar curvatures, and
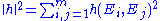
If , the scalar curvature equation might be more complicated.
, the scalar curvature equation might be more complicated.
We can already use these equations to draw some conclusions. For example, any minimal immersion into the round sphere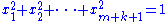 must be of the form
must be of the form
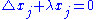
where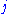 runs from 1 to
runs from 1 to 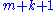 and
and
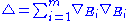
is the Laplacian on M, and is a positive constant.
is a positive constant.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, the Gauss–Codazzi–Mainardi equations are fundamental equations in the theory of embedded hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
s in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, and more generally submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
s of Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s. They also have applications for embedded hypersurfaces of pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
s: see Gauss–Codazzi equations (relativity).
In the classical differential geometry of surfaces
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
, the Gauss–Codazzi–Mainardi equations consist of a pair of related equations. The first equation, sometimes called the Gauss equation, relates the intrinsic curvature (or Gauss curvature) of the surface to the derivatives of the Gauss map
Gauss map
In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...
, via the second fundamental form. This equation is the basis for Gauss's theorema egregium
Theorema Egregium
Gauss's Theorema Egregium is a foundational result in differential geometry proved by Carl Friedrich Gauss that concerns the curvature of surfaces...
. The second equation, sometimes called the Codazzi–Mainardi equation, is a structural condition on the second derivatives of the Gauss map.
It was named for Gaspare Mainardi
Gaspare Mainardi
Gaspare Mainardi was an Italian mathematician active in Differential Geometry. He is remembered for the Gauss-Codazzi-Mainardi equations.-References:* Tricomi: La Matematica Italiana 1800-1950...
(1856) and Delfino Codazzi
Delfino Codazzi
Delfino Codazzi was an Italian mathematician. He made some important contributions to the differential geometry of surfaces, such as the Gauss–Codazzi–Mainardi equations.-External links:...
(1868–1869), who independently derived the result , although it was discovered earlier by .
It incorporates the extrinsic curvature (or mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
) of the surface. The equations show that the components of the second fundamental form and its derivatives along the surface completely classify the surface up to a Euclidean transformation, a theorem of Ossian Bonnet.
Formal statement
Let i : M ⊂ P be an n-dimensional embedded submanifold of a Riemannian manifold P of dimension n+p. There is a natural inclusion of the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of M into that of P by the pushforward, and the cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
is the normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
of M:
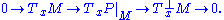
The metric splits this short exact sequence, and so
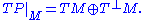
Relative to this splitting, the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
∇′ of P decomposes into tangential and normal components. For each X ∈ TM and vector field Y on M,
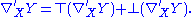
Let
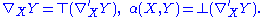
Gauss' formula now asserts that ∇X is the Levi-Civita connection for M, and α is a symmetric vector-valued form
Vector-valued form
In mathematics, a vector-valued differential form on a manifold M is a differential form on M with values in a vector space V. More generally, it is a differential form with values in some vector bundle E over M. Ordinary differential forms can be viewed as R-valued differential forms...
with values in the normal bundle. It is often referred to as the second fundamental form.
An immediate corollary is the Gauss equation. For X, Y, Z, W ∈ TM,
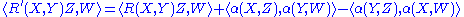
where R′ is the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
of P and R is that of M.
The Weingarten equation is an analog of the Gauss formula for a connection in the normal bundle. Let X ∈ TM and ξ a normal vector field. Then decompose the ambient covariant derivative of ξ along X into tangential and normal components:
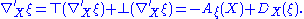
Then
- Weingarten's equation:

- DX is a metric connectionMetric connectionIn mathematics, a metric connection is a connection in a vector bundle E equipped with a metric for which the inner product of any two vectors will remain the same when those vectors are parallel transported along any curve...
in the normal bundle.
There are thus a pair of connections: ∇, defined on the tangent bundle of M; and D, defined on the normal bundle of M. These combine to form a connection on any tensor product of copies of TM and T⊥M. In particular, they defined the covariant derivative of α:
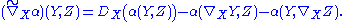
The Codazzi–Mainardi equation is
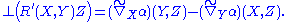
Since every immersion is, in particular, a local embedding, the above formulas also hold for immersions.
Statement of classical equations
In classical differential geometry of surfaces, the Codazzi–Mainardi equations are expressed via the second fundamental form (L, M, N):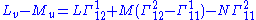
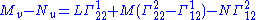
Derivation of classical equations
Consider a parametric surfaceParametric surface
A parametric surface is a surface in the Euclidean space R3 which is defined by a parametric equation with two parameters. Parametric representation is the most general way to specify a surface. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence...
in Euclidean space,
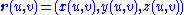
where the three component functions depend smoothly on ordered pairs (u,v) in some open domain U in the uv-plane. Assume that this surface is regular, meaning that the vectors ru and rv are linearly independent. Complete this to a basis{ru,rv,n}, by selecting a unit vector n normal to the surface. It is possible to express the second partial derivatives of r using the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
and the second fundamental form.
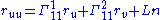
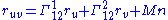
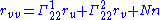
Clairaut's theorem states that partial derivatives commute:
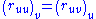
If we differentiate ruu with respect to v and ruv with respect to u, we get:
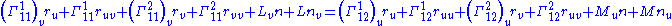
Now substitute the above expressions for the second derivatives and equate the coefficients of n:
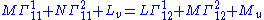
Rearranging this equation gives the first Codazzi–Mainardi equation.
The second equation may be derived similarly.
Mean curvature
Let M be a smooth m-dimensional manifold immersed in the (m + k)-dimensional smooth manifold P. Let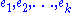 be a local orthonormal frame of vector fields normal to M. Then we can write,
be a local orthonormal frame of vector fields normal to M. Then we can write,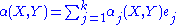
If, now,
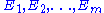 is a local orthonormal frame (of tangent vector fields) on the same open subset of M, then we can define the mean curvature
is a local orthonormal frame (of tangent vector fields) on the same open subset of M, then we can define the mean curvatureMean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
s of the immersion by
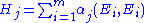
In particular, if M is a hypersurface of P, i.e.
 , then there is only one mean curvature to speak of. The immersion is called minimal
, then there is only one mean curvature to speak of. The immersion is called minimalMinimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
if all the
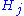 are identically zero.
are identically zero.Observe that the mean curvature is a trace, or average, of the second fundamental form, for any given component. Sometimes mean curvature is defined by multiplying the sum on the right-hand side by
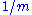 .
.We can now write the Gauss–Codazzi equations as
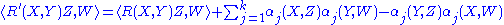
Contracting the
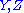 components gives us
components gives us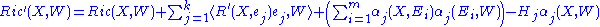
Observe that the tensor in parentheses is symmetric and nonnegative-definite in
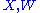 . Assuming that M is a hypersurface, this simplifies to
. Assuming that M is a hypersurface, this simplifies to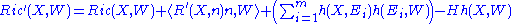
where
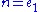 and
and 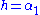 and
and 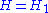 . In that case, one more contraction yields,
. In that case, one more contraction yields,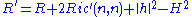
where
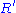 and
and 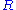 are the respective scalar curvatures, and
are the respective scalar curvatures, and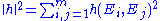
If
 , the scalar curvature equation might be more complicated.
, the scalar curvature equation might be more complicated.We can already use these equations to draw some conclusions. For example, any minimal immersion into the round sphere
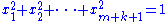 must be of the form
must be of the form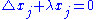
where
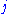 runs from 1 to
runs from 1 to 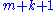 and
and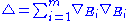
is the Laplacian on M, and
 is a positive constant.
is a positive constant.
