
List of knapsack problems
Encyclopedia
The knapsack problem
is one of the most studied problems in combinatorial optimization
, with many real-life applications. For this reason, many special cases and generalizations have been examined.
Common to all versions are a set of n items, with each item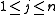 having an associated profit pj and weight wj. The objective is to pick some of the items, with maximal total profit, while obeying that the maximum total weight of the chosen items must not exceed W. Generally, these coefficients are scaled to become integers, and they are almost always assumed to be positive.
having an associated profit pj and weight wj. The objective is to pick some of the items, with maximal total profit, while obeying that the maximum total weight of the chosen items must not exceed W. Generally, these coefficients are scaled to become integers, and they are almost always assumed to be positive.
The knapsack problem in its most basic form:
The unbounded knapsack problem (sometimes called the integer knapsack problem) does not put any upper bounds on the number of times an item may be selected:
The unbounded variant was shown to be NP-complete
in 1975 by Lueker. Both the bounded and unbounded variants admit an FPTAS
(essentially the same as the one used in the 0-1 knapsack problem).
If the items are subdivided into k classes denoted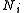 , and exactly one item must be taken from each class, we get the multiple-choice knapsack problem:
, and exactly one item must be taken from each class, we get the multiple-choice knapsack problem:
If for each item the profits and weights are identical, we get the subset sum problem (often the corresponding decision problem
is given instead):
If we have n items and m knapsacks with capacities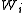 , we get the multiple knapsack problem:
, we get the multiple knapsack problem:
Quadratic knapsack problem:
The Set-Union Knapsack Problem:
SUKP is defined as follows: Given a set of items
items 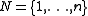 and a set of
and a set of 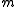 so called elements
so called elements 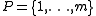 , each item
, each item 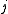 corresponds to a subset
corresponds to a subset 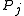 of the element set
of the element set 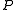 . The items
. The items 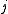 have non-negative profits
have non-negative profits  ,
,  , and the elements
, and the elements 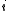 have non-negative weights
have non-negative weights 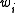 ,
, 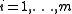 . The total weight of a set of items is given by the total weight of the elements of the union of the corresponding element sets. The objective is to find a subset of the items with total weight not exceeding the knapsack capacity and maximal profit.
. The total weight of a set of items is given by the total weight of the elements of the union of the corresponding element sets. The objective is to find a subset of the items with total weight not exceeding the knapsack capacity and maximal profit.
The 0-1 variant (for any fixed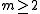 ) was shown to be NP-complete
) was shown to be NP-complete
around 1980 and more strongly, has no FPTAS unless P=NP.
The bounded and unbounded variants (for any fixed ) also exhibit the same hardness.
) also exhibit the same hardness.
For any fixed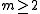 , these problems do admit a pseudo-polynomial time
, these problems do admit a pseudo-polynomial time
algorithm (similar to the one for basic knapsack) and a PTAS
.
If we have a number of containers (of the same size), and we wish to pack all n items in as few containers as possible, we get the bin packing problem
, which is modelled by having indicator variables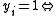 container i is being used:
container i is being used:
The cutting stock problem
is identical to the bin packing problem
, but since practical instances usually have far fewer types of items, another formulation is often used. Item j is needed Bj times, each "pattern" of items which fit into a single knapsack have a variable, xi (there are m patterns), and pattern i uses item j bij times:
If, to the multiple choice knapsack problem, we add the constraint that each subset is of size n and remove the restriction on total weight, we get the assignment problem
, which is also the problem of finding a maximal bipartite matching:
Although less common than those above, several other knapsack-like problems exist, including:
Knapsack problem
The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
is one of the most studied problems in combinatorial optimization
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
, with many real-life applications. For this reason, many special cases and generalizations have been examined.
Common to all versions are a set of n items, with each item
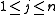 having an associated profit pj and weight wj. The objective is to pick some of the items, with maximal total profit, while obeying that the maximum total weight of the chosen items must not exceed W. Generally, these coefficients are scaled to become integers, and they are almost always assumed to be positive.
having an associated profit pj and weight wj. The objective is to pick some of the items, with maximal total profit, while obeying that the maximum total weight of the chosen items must not exceed W. Generally, these coefficients are scaled to become integers, and they are almost always assumed to be positive.The knapsack problem in its most basic form:
maximize  |
||
| subject to | 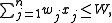 |
|
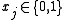 |
 |
Direct generalizations
One common variant is that each item can be chosen multiple times. The bounded knapsack problem specifies, for each item j, an upper bound uj (which may be a positive integer, or infinity) on the number of times item j can be selected:maximize 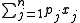 |
||
| subject to |  |
|
 integral for all j integral for all j |
The unbounded knapsack problem (sometimes called the integer knapsack problem) does not put any upper bounds on the number of times an item may be selected:
maximize 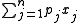 |
||
| subject to | 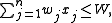 |
|
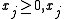 integral for all j integral for all j |
The unbounded variant was shown to be NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
in 1975 by Lueker. Both the bounded and unbounded variants admit an FPTAS
Polynomial-time approximation scheme
In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....
(essentially the same as the one used in the 0-1 knapsack problem).
If the items are subdivided into k classes denoted
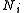 , and exactly one item must be taken from each class, we get the multiple-choice knapsack problem:
, and exactly one item must be taken from each class, we get the multiple-choice knapsack problem:maximize 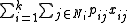 |
||
| subject to | 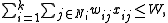 |
|
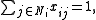 |
for all 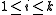 |
|
 |
for all 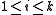 and all and all 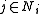 |
If for each item the profits and weights are identical, we get the subset sum problem (often the corresponding decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
is given instead):
maximize 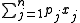 |
||
| subject to | 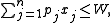 |
|
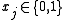 |
If we have n items and m knapsacks with capacities
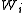 , we get the multiple knapsack problem:
, we get the multiple knapsack problem:maximize 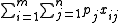 |
||
| subject to |  |
for all 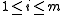 |
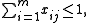 |
for all  |
|
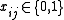 |
for all 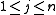 and all and all 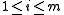 |
Quadratic knapsack problem:
maximize 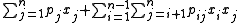 |
|||
| subject to | 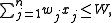 |
||
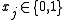 |
for all 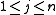 |
The Set-Union Knapsack Problem:
SUKP is defined as follows: Given a set of
 items
items 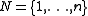 and a set of
and a set of 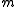 so called elements
so called elements 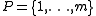 , each item
, each item 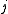 corresponds to a subset
corresponds to a subset 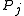 of the element set
of the element set 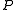 . The items
. The items 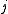 have non-negative profits
have non-negative profits  ,
,  , and the elements
, and the elements 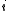 have non-negative weights
have non-negative weights 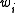 ,
, 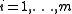 . The total weight of a set of items is given by the total weight of the elements of the union of the corresponding element sets. The objective is to find a subset of the items with total weight not exceeding the knapsack capacity and maximal profit.
. The total weight of a set of items is given by the total weight of the elements of the union of the corresponding element sets. The objective is to find a subset of the items with total weight not exceeding the knapsack capacity and maximal profit.Multiple constraints
If there is more than one constraint (for example, both a volume limit and a weight limit, where the volume and weight of each item are not related), we get the multiply constrained knapsack problem, multi-dimensional knapsack problem, or m-dimensional knapsack problem. (Note, "dimension" here does not refer to the shape of any items.) This has 0-1, bounded, and unbounded variants; the unbounded one is shown below.maximize  |
||
| subject to | 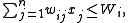 |
for all  |
 , , 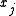 integer integer |
for all 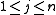 |
The 0-1 variant (for any fixed
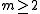 ) was shown to be NP-complete
) was shown to be NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
around 1980 and more strongly, has no FPTAS unless P=NP.
The bounded and unbounded variants (for any fixed
 ) also exhibit the same hardness.
) also exhibit the same hardness.For any fixed
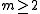 , these problems do admit a pseudo-polynomial time
, these problems do admit a pseudo-polynomial timePseudo-polynomial time
In computational complexity theory, a numeric algorithm runs in pseudo-polynomial time if its running time is polynomial in the numeric value of the input ....
algorithm (similar to the one for basic knapsack) and a PTAS
Polynomial-time approximation scheme
In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....
.
Knapsack-like problems
If all the profits are 1, we can try to minimize the number of items which exactly fill the knapsack:minimize 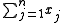 |
||
| subject to | 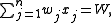 |
|
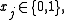 |
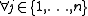 |
If we have a number of containers (of the same size), and we wish to pack all n items in as few containers as possible, we get the bin packing problem
Bin packing problem
In computational complexity theory, the bin packing problem is a combinatorial NP-hard problem. In it, objects of different volumes must be packed into a finite number of bins of capacity V in a way that minimizes the number of bins used....
, which is modelled by having indicator variables
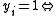 container i is being used:
container i is being used:minimize 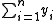 |
||
| subject to | 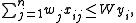 |
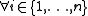 |
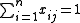 |
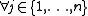 |
|
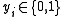 |
 |
|
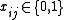 |
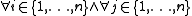 |
The cutting stock problem
Cutting stock problem
The cutting-stock problem is an optimization problem, or more specifically, an integer linear programming problem. It arises from many applications in industry. Imagine that you work in a paper mill and you have a number of rolls of paper of fixed width waiting to be cut, yet different customers...
is identical to the bin packing problem
Bin packing problem
In computational complexity theory, the bin packing problem is a combinatorial NP-hard problem. In it, objects of different volumes must be packed into a finite number of bins of capacity V in a way that minimizes the number of bins used....
, but since practical instances usually have far fewer types of items, another formulation is often used. Item j is needed Bj times, each "pattern" of items which fit into a single knapsack have a variable, xi (there are m patterns), and pattern i uses item j bij times:
minimize 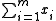 |
||
| subject to | 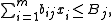 |
for all 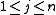 |
 |
for all  |
If, to the multiple choice knapsack problem, we add the constraint that each subset is of size n and remove the restriction on total weight, we get the assignment problem
Assignment problem
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics...
, which is also the problem of finding a maximal bipartite matching:
minimize 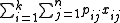 |
||
| subject to |  |
for all 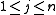 |
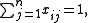 |
for all 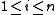 |
|
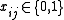 |
for all  and all and all 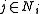 |
Although less common than those above, several other knapsack-like problems exist, including:
- Collapsing knapsack problem
- Nested knapsack problem
- Nonlinear knapsack problem
- Inverse-parametric knapsack problem

