
Local Tate duality
Encyclopedia
In Galois cohomology
, local Tate duality (or simply local duality) is a duality
for Galois module
s for the absolute Galois group
of a non-archimedean local field. It is named after John Tate
who first proved it. It shows that the dual
of such a Galois module is the Tate twist
of usual linear dual. This new dual is called the (local) Tate dual.
Local duality combined with Tate's local Euler characteristic formula
provide a versatile set of tools for computing the Galois cohomology of local fields.
of K), the Tate dual of A is defined as
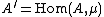
(i.e. it is the Tate twist of the usual dual A∗). Let Hi(K, A) denote the group cohomology
of GK with coefficients in A. The theorem states that the pairing
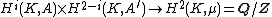
given by the cup product
sets up a duality between Hi(K, A) and H2−i(K, A′) for i = 0, 1, 2. Since GK has cohomological dimension
equal to two, the higher cohomology groups vanish.
. Let Qp(1) denote the p-adic cyclotomic character
of GK (i.e. the Tate module
of μ). A p-adic representation of GK is a continuous representation

where V is a finite-dimensional vector space
over the p-adic number
s Qp and GL(V) denotes the group of invertible linear maps from V to itself. The Tate dual of V is defined as
(i.e. it is the Tate twist of the usual dual V∗ = Hom(V, Qp)). In this case, Hi(K, V) denotes the continuous group cohomology of GK with coefficients in V. Local Tate duality applied to V says that the cup product induces a pairing
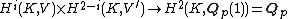
which is a duality between Hi(K, V) and H2−i(K, V ′) for i = 0, 1, 2. Again, the higher cohomology groups vanish.
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
, local Tate duality (or simply local duality) is a duality
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
for Galois module
Galois module
In mathematics, a Galois module is a G-module where G is the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring, but can also be used as a synonym for G-module...
s for the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
of a non-archimedean local field. It is named after John Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
who first proved it. It shows that the dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
of such a Galois module is the Tate twist
Tate twist
In number theory and algebraic geometry, the Tate twist, named after John Tate, is an operation on Galois modules.For example, if K is a field, GK is its absolute Galois group, and ρ : GK → AutK is a representation of GK on a finite-dimensional vector space V over the field Qp of p-adic numbers,...
of usual linear dual. This new dual is called the (local) Tate dual.
Local duality combined with Tate's local Euler characteristic formula
Local Euler characteristic formula
In the mathematical field of Galois cohomology, the local Euler characteristic formula is a result due to John Tate that computes the Euler characteristic of the group cohomology of the absolute Galois group GK of a non-archimedean local field K....
provide a versatile set of tools for computing the Galois cohomology of local fields.
Statement
Let K be a non-archimedean local field, let Ks denote a separable closure of K, and let GK = Gal(Ks/K) be the absolute Galois group of K.Case of finite modules
Denote by μ the Galois module of all roots of unity in Ks. Given a finite GK-module A (of order prime to the characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of K), the Tate dual of A is defined as
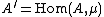
(i.e. it is the Tate twist of the usual dual A∗). Let Hi(K, A) denote the group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
of GK with coefficients in A. The theorem states that the pairing
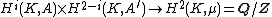
given by the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
sets up a duality between Hi(K, A) and H2−i(K, A′) for i = 0, 1, 2. Since GK has cohomological dimension
Cohomological dimension
In abstract algebra, cohomological dimension is an invariant which measures the homological complexity of representations of a group. It has important applications in geometric group theory, topology, and algebraic number theory....
equal to two, the higher cohomology groups vanish.
Case of p-adic representations
Let p be a prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. Let Qp(1) denote the p-adic cyclotomic character
Cyclotomic character
In number theory, a cyclotomic character is a character of a Galois group giving the Galois action on a group of roots of unity. As a one-dimensional representation over a ring R, its representation space is generally denoted by R .-p-adic cyclotomic character:If p is a prime, and G is the absolute...
of GK (i.e. the Tate module
Tate module
In mathematics, a Tate module of an abelian group, named for John Tate, is a module constructed from an abelian group A. Often, this construction is made in the following situation: G is a commutative group scheme over a field K, Ks is the separable closure of K, and A = G...
of μ). A p-adic representation of GK is a continuous representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...

where V is a finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the p-adic number
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s Qp and GL(V) denotes the group of invertible linear maps from V to itself. The Tate dual of V is defined as

(i.e. it is the Tate twist of the usual dual V∗ = Hom(V, Qp)). In this case, Hi(K, V) denotes the continuous group cohomology of GK with coefficients in V. Local Tate duality applied to V says that the cup product induces a pairing
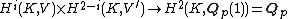
which is a duality between Hi(K, V) and H2−i(K, V ′) for i = 0, 1, 2. Again, the higher cohomology groups vanish.

