
Cyclotomic character
Encyclopedia
In number theory
, a cyclotomic character is a character of a Galois group
giving the Galois action
on a group
of roots of unity. As a one-dimensional representation
over a ring
R, its representation space is generally denoted by R(1) (that is, it is a representation ).
, and G is the absolute Galois group
of the rational number
s, the p-adic cyclotomic character is a group homomorphism

where Zp× is the group of units of the ring of p-adic integers. This homomorphism is defined as follows. Let ζn be a primitive pn root of unity. Every pn root of unity is a power of ζn uniquely defined as an element of the ring of integers modulo pn. Primitive roots of unity correspond to the invertible elements
, i.e. to (Z/pn)×. An element g of the Galois group G sends ζn to another primitive pn root of unity

where ag,n ∈ (Z/pn)×. For a given g, as n varies, the ag,n form a comptatible system in the sense that they give an element of the inverse limit
of the (Z/pn)×. This inverse limit is exactly Zp×. Therefore, the p-adic cyclotomic character sends g to the system (ag,n)n, thus encoding the action of g on all p-power roots of unity.
In fact, χp is a continuous
homomorphism (where the topology
on G is the Krull topology, and that on Zp× is the profinite topology).
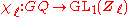
satisfying certain compatibilities between different primes. In fact, the χℓ form a strictly compatible system of ℓ-adic representations.
The p-adic cyclotomic character is the p-adic Tate module
of the multiplicative group scheme
Gm,Q over Q. As such, its representation space can be viewed as the inverse limit
of the groups of pnth roots of unity in .
In terms of cohomology
, the p-adic cyclotomic character is the dual
of the first p-adic étale cohomology
group of Gm. It can also be found in the étale cohomology of a projective variety, namely the projective line
: it is the dual of H2ét( P1 ).
In terms of motives
, the p-adic cyclotomic character is the p-adic realization of the Tate motive Z(1). As a Grothendieck motive, the Tate motive is the dual of H2( P1 ).
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a cyclotomic character is a character of a Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
giving the Galois action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of roots of unity. As a one-dimensional representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R, its representation space is generally denoted by R(1) (that is, it is a representation ).
p-adic cyclotomic character
If p is a primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, and G is the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
of the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, the p-adic cyclotomic character is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...

where Zp× is the group of units of the ring of p-adic integers. This homomorphism is defined as follows. Let ζn be a primitive pn root of unity. Every pn root of unity is a power of ζn uniquely defined as an element of the ring of integers modulo pn. Primitive roots of unity correspond to the invertible elements
Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
, i.e. to (Z/pn)×. An element g of the Galois group G sends ζn to another primitive pn root of unity

where ag,n ∈ (Z/pn)×. For a given g, as n varies, the ag,n form a comptatible system in the sense that they give an element of the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the (Z/pn)×. This inverse limit is exactly Zp×. Therefore, the p-adic cyclotomic character sends g to the system (ag,n)n, thus encoding the action of g on all p-power roots of unity.
In fact, χp is a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
homomorphism (where the topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
on G is the Krull topology, and that on Zp× is the profinite topology).
As a compatible system of ℓ-adic representations
By varying ℓ over all prime numbers, a compatible system of ℓ-adic representations is obtained from the ℓ-adic cyclotomic characters (when considering compatible systems of representations, the standard terminology is to use the symbol ℓ to denote a prime instead of p). That is to say, χ = { χℓ }ℓ is a "family" of ℓ-adic representations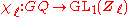
satisfying certain compatibilities between different primes. In fact, the χℓ form a strictly compatible system of ℓ-adic representations.
Geometric realizations
The p-adic cyclotomic character is the p-adic Tate module
Tate module
In mathematics, a Tate module of an abelian group, named for John Tate, is a module constructed from an abelian group A. Often, this construction is made in the following situation: G is a commutative group scheme over a field K, Ks is the separable closure of K, and A = G...
of the multiplicative group scheme
Algebraic torus
In mathematics, an algebraic torus is a type of commutative affine algebraic group. These groups were named by analogy with the theory of tori in Lie group theory...
Gm,Q over Q. As such, its representation space can be viewed as the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the groups of pnth roots of unity in .
In terms of cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
, the p-adic cyclotomic character is the dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
of the first p-adic étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
group of Gm. It can also be found in the étale cohomology of a projective variety, namely the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
: it is the dual of H2ét( P1 ).
In terms of motives
Motive (algebraic geometry)
In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
, the p-adic cyclotomic character is the p-adic realization of the Tate motive Z(1). As a Grothendieck motive, the Tate motive is the dual of H2( P1 ).
Properties
The p-adic cyclotomic character satisfies several nice properties.- It is unramified at all primes ℓ ≠ p (i.e. the inertia subgroup at ℓ acts trivially).
- If Frobℓ is a Frobenius element for ℓ ≠ p, then χp(Frobℓ) = ℓ
- It is crystalline at p.

