Local parameter
Encyclopedia
In the geometry of complex algebraic curve
s, a local parameter for a curve C at a smooth point P is just a meromorphic function
on C that has a simple zero at P. This concept can be generalized to curves defined over fields other than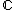
(or even scheme
s), because the local ring
at a smooth point P of an algebraic curve C (defined over an algebraically closed field
) is always a discrete valuation ring
. This valuation will endow us with a way to count the order (at the point P) of rational functions (which are natural generalizations for meromorphic functions in the non-complex realm) having a zero or a pole at P.
Local parameters, as its name indicates, are used mainly to properly count multiplicities in a local way.
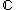, we do not have access to the power of the complex analysis, and a replacement must be found in order to define multiplicities of zeroes and poles of rational functions defined on such curves. In this last case, we say that the germ of the regular function 
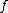vanishes at 
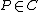if 
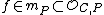. This is in complete analogy with the complex case, in which the maximal ideal of the local ring at a point P is actually conformed by the germs of holomorphic functions vanishing at P.
Now, the valuation function on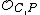
is given by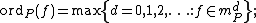
this valuation can naturally be extended to K(C) (which is the field of rational functions of C) because it is the field of fractions
of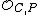
. Hence the idea of having a simple zero at a point P is now complete: it will be a rational function 
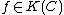such that its germ falls into 
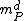, with d at most 1.
This has an algebraic resemblance with the concept of a uniformizing parameter (or just uniformizer) found in the context of discrete valuation ring
s in commutative algebra
; a uniformizing parameter for the DVR (R, m) is just a generator of the maximal ideal m. The link comes from the fact that a local parameter at P will be a uniformizing parameter for the DVR (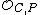
, 
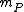), whence the name.
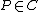is defined as
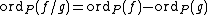, where 
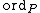is the usual valuation on the local ring (
, 
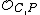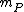). A local parameter for C at P is a function 
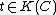such that 
.
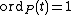Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s, a local parameter for a curve C at a smooth point P is just a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
on C that has a simple zero at P. This concept can be generalized to curves defined over fields other than
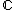(or even schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
s), because the local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
at a smooth point P of an algebraic curve C (defined over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
) is always a discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
. This valuation will endow us with a way to count the order (at the point P) of rational functions (which are natural generalizations for meromorphic functions in the non-complex realm) having a zero or a pole at P.
Local parameters, as its name indicates, are used mainly to properly count multiplicities in a local way.
Introduction
When C is a complex algebraic curve, we know how to count multiplicities of zeroes and poles of meromorphic functions defined on it. However, when discussing curves defined over fields other than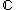, we do not have access to the power of the complex analysis, and a replacement must be found in order to define multiplicities of zeroes and poles of rational functions defined on such curves. In this last case, we say that the germ of the regular function 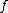vanishes at 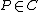if 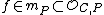. This is in complete analogy with the complex case, in which the maximal ideal of the local ring at a point P is actually conformed by the germs of holomorphic functions vanishing at P.Now, the valuation function on
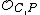is given by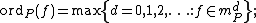this valuation can naturally be extended to K(C) (which is the field of rational functions of C) because it is the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of
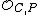. Hence the idea of having a simple zero at a point P is now complete: it will be a rational function 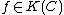such that its germ falls into 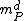, with d at most 1.This has an algebraic resemblance with the concept of a uniformizing parameter (or just uniformizer) found in the context of discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
s in commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
; a uniformizing parameter for the DVR (R, m) is just a generator of the maximal ideal m. The link comes from the fact that a local parameter at P will be a uniformizing parameter for the DVR (
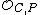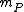, ), whence the name.Definition
Let C be an algebraic curve defined over an algebraically closed field K, and let K(C) be the field of rational functions of C. The valuation on K(C) corresponding to a smooth point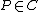 is defined as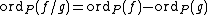, where 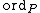is the usual valuation on the local ring (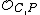, 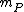). A local parameter for C at P is a function 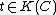such that .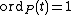