Locally simply connected space
Encyclopedia
In mathematics
, a locally simply connected space is a topological space
that admits a basis
of simply connected sets. Every locally simply connected space is also locally path-connected and locally connected.
 The circle
The circle
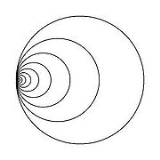
is an example of a locally simply connected space which is not simply connected. The Hawaiian earring
is a space which is neither locally simply connected nor simply connected. The cone
on the Hawaiian earring is contractible
and therefore simply connected, but still not locally simply connected.
All topological manifold
s and CW complex
es are locally simply connected. In fact, these satisfy the much stronger property of being locally contractible.
A strictly weaker condition is that of being semi-locally simply connected
. Both locally simply connected spaces and simply connected spaces are semi-locally simply connected, but neither converse holds.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a locally simply connected space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that admits a basis
Basis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
of simply connected sets. Every locally simply connected space is also locally path-connected and locally connected.

Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is an example of a locally simply connected space which is not simply connected. The Hawaiian earring
Hawaiian earring
In mathematics, the Hawaiian earring H is the topological space defined by the union of circles in the Euclidean plane R2 with center and radius 1/n for n = 1, 2, 3, ......
is a space which is neither locally simply connected nor simply connected. The cone
Cone (topology)
In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
on the Hawaiian earring is contractible
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
and therefore simply connected, but still not locally simply connected.
All topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
s and CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es are locally simply connected. In fact, these satisfy the much stronger property of being locally contractible.
A strictly weaker condition is that of being semi-locally simply connected
Semi-locally simply connected
In mathematics, specifically algebraic topology, the phrase semi-locally simply connected refers to a certain local connectedness condition that arises in the theory of covering spaces. Roughly speaking, a topological space X is semi-locally simply connected if there is a lower bound on the sizes...
. Both locally simply connected spaces and simply connected spaces are semi-locally simply connected, but neither converse holds.

