Luzin N property
Encyclopedia
In mathematics
, a function f on the interval [a, b] has the Luzin N property, named after Nikolai Luzin
(also called Luzin property or N property) if for all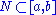
such that 
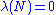, there holds: 
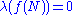, where 
stands for the Lebesgue measure
.
Note that the image of such a set N is not necessarily measurable, but since the Lebesgue measure is complete
, it follows that if the Lebesgue outer measure
of that set is zero, then it is measurable and its Lebesgue measure is zero as well.
on the other hand does not: the Lebesgue measure of the Cantor set
is zero, however its image is the complete [0,1] interval.
Also, if a function f on the interval [a,b] is continuous
, is of bounded variation
and has the Luzin N property, then it is absolutely continuous.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a function f on the interval [a, b] has the Luzin N property, named after Nikolai Luzin
Nikolai Luzin
Nikolai Nikolaevich Luzin, , was a Soviet/Russian mathematician known for his work in descriptive set theory and aspects of mathematical analysis with strong connections to point-set topology. He was the eponym of Luzitania, a loose group of young Moscow mathematicians of the first half of the...
(also called Luzin property or N property) if for all
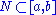such that 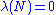, there holds: 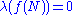, where stands for the Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
.
Note that the image of such a set N is not necessarily measurable, but since the Lebesgue measure is complete
Complete measure
In mathematics, a complete measure is a measure space in which every subset of every null set is measurable...
, it follows that if the Lebesgue outer measure
Outer measure
In mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by...
of that set is zero, then it is measurable and its Lebesgue measure is zero as well.
Properties
Every absolutely continuous function has the Luzin N property. The Cantor functionCantor function
In mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
on the other hand does not: the Lebesgue measure of the Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
is zero, however its image is the complete [0,1] interval.
Also, if a function f on the interval [a,b] is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, is of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
and has the Luzin N property, then it is absolutely continuous.