
MDS matrix
Encyclopedia
An MDS matrix is a matrix
representing a function with certain diffusion properties that have useful applications in cryptography
. Technically, an m×n matrix A over a finite field
K is an MDS matrix if it is the transformation matrix
of a linear transformation
f(x)=Ax from Kn to Km such that no two different (m+n)-tuples of the form (x,f(x)) coincide in n or more components.
Equivalently, the set of all (m+n)-tuples (x,f(x)) is an MDS code, i.e. a linear code
that reaches the Singleton bound
.
Let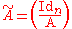 be the matrix obtained by joining the identity matrix
be the matrix obtained by joining the identity matrix
Idn to A.
Then a necessary and sufficient condition for a matrix A to be MDS is that every possible n×n submatrix obtained by removing m rows from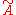
is non-singular.
Reed-Solomon codes have the MDS property and are frequently used to obtain the MDS matrices used in cryptographic algorithms.
Serge Vaudenay
suggested using MDS matrices in cryptographic primitive
s to produce what he called multipermutations, not-necessarily linear functions with this same property. These functions have what he called perfect diffusion: changing t of the inputs changes at least m-t+1 of the outputs. He showed how to exploit imperfect diffusion to cryptanalyze
functions that are not multipermutations.
MDS matrices are used for diffusion in such block cipher
s as AES
, SHARK
, Square
, Twofish
, Manta, Hierocrypt
, and Camellia
, and in the stream cipher
MUGI
and the cryptographic hash function
WHIRLPOOL
.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
representing a function with certain diffusion properties that have useful applications in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
. Technically, an m×n matrix A over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
K is an MDS matrix if it is the transformation matrix
of a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
f(x)=Ax from Kn to Km such that no two different (m+n)-tuples of the form (x,f(x)) coincide in n or more components.
Equivalently, the set of all (m+n)-tuples (x,f(x)) is an MDS code, i.e. a linear code
Linear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
that reaches the Singleton bound
Singleton bound
In coding theory, the Singleton bound, named after Richard Collom Singleton, is a relatively crude bound on the size of a block code C with block length n, size r and minimum distance d.-Statement of the Bound:...
.
Let
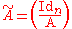 be the matrix obtained by joining the identity matrix
be the matrix obtained by joining the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
Idn to A.
Then a necessary and sufficient condition for a matrix A to be MDS is that every possible n×n submatrix obtained by removing m rows from
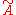
is non-singular.
Reed-Solomon codes have the MDS property and are frequently used to obtain the MDS matrices used in cryptographic algorithms.
Serge Vaudenay
Serge Vaudenay
Serge Vaudenay is a well-known French cryptographer.Serge Vaudenay entered the École Normale Supérieure in Paris as a normalien student in 1989. In 1992, he passed the agrégation in mathematics. He did his PhD at the computer science laboratory of École Normale Supérieure, and defended it in 1995...
suggested using MDS matrices in cryptographic primitive
Cryptographic primitive
Cryptographic primitives are well-established, low-level cryptographic algorithms that are frequently used to build computer security systems. These routines include, but are not limited to, one-way hash functions and encryption functions.- Rationale :...
s to produce what he called multipermutations, not-necessarily linear functions with this same property. These functions have what he called perfect diffusion: changing t of the inputs changes at least m-t+1 of the outputs. He showed how to exploit imperfect diffusion to cryptanalyze
Cryptanalysis
Cryptanalysis is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key...
functions that are not multipermutations.
MDS matrices are used for diffusion in such block cipher
Block cipher
In cryptography, a block cipher is a symmetric key cipher operating on fixed-length groups of bits, called blocks, with an unvarying transformation. A block cipher encryption algorithm might take a 128-bit block of plaintext as input, and output a corresponding 128-bit block of ciphertext...
s as AES
Advanced Encryption Standard
Advanced Encryption Standard is a specification for the encryption of electronic data. It has been adopted by the U.S. government and is now used worldwide. It supersedes DES...
, SHARK
SHARK
In cryptography, SHARK is a block cipher identified as one of the predecessors of Rijndael .SHARK has a 64-bit block size and a 128-bit key size. It is a six round SP-network which alternates a key mixing stage with linear and non-linear transformation layers...
, Square
Square (cipher)
In cryptography, Square is a block cipher invented by Joan Daemen and Vincent Rijmen. The design, published in 1997, is a forerunner to the Rijndael algorithm, which has been adopted as the Advanced Encryption Standard...
, Twofish
Twofish
In cryptography, Twofish is a symmetric key block cipher with a block size of 128 bits and key sizes up to 256 bits. It was one of the five finalists of the Advanced Encryption Standard contest, but was not selected for standardisation...
, Manta, Hierocrypt
Hierocrypt
In cryptography, Hierocrypt-L1 and Hierocrypt-3 are block ciphers created byToshiba in 2000. They were submitted to the NESSIE project, but were not selected...
, and Camellia
Camellia (cipher)
In cryptography, Camellia is a 128-bit block cipher jointly developed by Mitsubishi and NTT. The cipher has been approved for use by the ISO/IEC, the European Union's NESSIE project and the Japanese CRYPTREC project...
, and in the stream cipher
Stream cipher
In cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
MUGI
MUGI
In cryptography, MUGI is a pseudorandom number generator designed for use as a stream cipher. It has been recommended for Japanese government use by the CRYPTREC project.MUGI takes a 128-bit secret key and a 128-bit initial vector...
and the cryptographic hash function
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
WHIRLPOOL
WHIRLPOOL
In computer science and cryptography, Whirlpool is a cryptographic hash function designed by Vincent Rijmen and Paulo S. L. M. Barreto first described in 2000. The hash has been recommended by the NESSIE project...
.

