Magnetic radiation reaction force
Encyclopedia
In the physics
of electromagnetism
, one can derive an electric radiation reaction force for an accelerating
charged particle
caused by the particle emitting electromagnetic radiation
. Likewise, a magnetic radiation reaction force can be derived for an accelerating magnetic moment
emitting electromagnetic radiation
.
Similar to the electric radiation reaction force, three conditions must be met in order to derive the following formula for the magnetic radiation reaction force. First, the motion of the magnetic moment
must be periodic, an assumption used to derive the force. Second, the magnetic moment is traveling at non-relativistic
velocities (that is, much slower than the speed of light
). Finally, this only applies to the realm of classical physics.
Since the magnetic moment is proportional to velocity, this force is proportional to the fifth derivative of the position as a function of time (sometimes somewhat facetiously referred to as the "Crackle"). Unlike the Abraham–Lorentz force, the force points in the direction opposite of the "Crackle".
where:
Note that this formula applies only for non-relativistic velocities.
Physically, a time changing magnetic moment emits radiation similar to the Larmor formula
of an accelerating charge. Since momentum is conserved, the magnetic moment is pushed in the direction opposite the direction of the emitted radiation. In fact the formula above for radiation force can be derived from the magnetic version of the Larmor formula, as shown below.
In some fields of physics, such as plasma physics and the calculation of transport coefficients (conductivity, diffusivity, etc.), the fields generated by the sources and the motion of the sources are solved self-consistently. In such cases, however, the motion of a selected source is calculated in response to fields generated by all other sources. Rarely is the motion of a particle (source) due to the fields generated by that same particle calculated. The reason for this is twofold:
This conceptual problems created by self-fields are highlighted in a standard graduate text. [Jackson]
The magnetic radiation reaction force is the result of the most fundamental calculation of the effect of self-generated fields. It arises from the observation that accelerating non-relativistic particles with associated magnetic moment emit radiation. The Abraham–Lorentz force is the average force that an accelerating charged particle feels in the recoil from the emission of radiation. The introduction of quantum effects
leads one to quantum electrodynamics
. The self-fields in quantum electrodynamics generate a finite number of infinities in the calculations that can be removed by the process of renormalization
. This has led to a theory that is able to make the most accurate predictions that humans have made to date. See precision tests of QED
. The renormalization process fails, however, when applied to the gravitational force. The infinities in that case are infinite in number, which causes the failure of renormalization. Therefore general relativity
has unsolved self-field problems. String theory
is a current attempt to resolve these problems for all forces.
for radiation of the second derivative of a magnetic moment with respect to time:
.
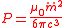In the case that the magnetic moment is produced by an electric charge moving along a circular path is
where
is the position of the charge 
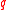relative to the center of the circle and 
is the instantaneous velocity of the charge.
The above Larmor formula
becomes as follows:
.
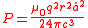If we assume the motion of a charged particle is periodic, then the average work done on the particle by the Abraham–Lorentz force is the negative of the Larmor power integrated over one period from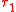
to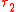 
:
.
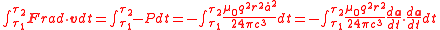Notice that we can integrate the above expression by parts. If we assume that there is periodic motion, the boundary term in the integral by parts disappears:
.
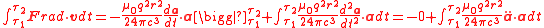Integrating by parts a second time, we find
.
Clearly, we can identify
.
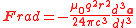and its relativistic counterpart quantum field theory
. See the quote from Rohrlich in the introduction concerning "the importance of obeying the validity limits of a physical theory".
For a particle in an external force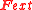
, we have
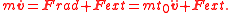
where
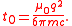
This equation can be integrated once to obtain
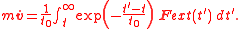
The integral extends from the present to infinitely far in the future. Thus future values of the force affect the acceleration of the particle in the present. The future values are weighted by the factor
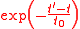
which falls off rapidly for times greater than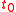
in the future. Therefore, signals from an interval approximately 
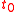into the future affect the acceleration in the present. For an electron, this time is approximately 
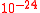sec, which is the time it takes for a light wave to travel across the "size" of an electron.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, one can derive an electric radiation reaction force for an accelerating
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
charged particle
Charged particle
In physics, a charged particle is a particle with an electric charge. It may be either a subatomic particle or an ion. A collection of charged particles, or even a gas containing a proportion of charged particles, is called a plasma, which is called the fourth state of matter because its...
caused by the particle emitting electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
. Likewise, a magnetic radiation reaction force can be derived for an accelerating magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
emitting electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
.
Similar to the electric radiation reaction force, three conditions must be met in order to derive the following formula for the magnetic radiation reaction force. First, the motion of the magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
must be periodic, an assumption used to derive the force. Second, the magnetic moment is traveling at non-relativistic
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
velocities (that is, much slower than the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
). Finally, this only applies to the realm of classical physics.
Since the magnetic moment is proportional to velocity, this force is proportional to the fifth derivative of the position as a function of time (sometimes somewhat facetiously referred to as the "Crackle"). Unlike the Abraham–Lorentz force, the force points in the direction opposite of the "Crackle".
Definition and description
Mathematically, the Abraham–Lorentz force is given by:-
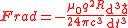(SISiSi, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units)
where:
- F is the force,
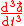is the Pop (the third derivative of accelerationAccelerationIn physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
, or the sixth derivative of displacementDisplacement (vector)A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
), - μ0 is the permeability of free space,
- c is the speed of light in free space
- q is the electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
of the particle. - R is the radius of the magnetic moment
Note that this formula applies only for non-relativistic velocities.
Physically, a time changing magnetic moment emits radiation similar to the Larmor formula
Larmor formula
In physics, in the area of electrodynamics, the Larmor formula is used to calculate the total power radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J...
of an accelerating charge. Since momentum is conserved, the magnetic moment is pushed in the direction opposite the direction of the emitted radiation. In fact the formula above for radiation force can be derived from the magnetic version of the Larmor formula, as shown below.
Background
In classical electrodynamics, problems are typically divided into two classes:- Problems in which the charge and current sources of fields are specified and the fields are calculated, and
- The reverse situation, problems in which the fields are specified and the motion of particles are calculated.
In some fields of physics, such as plasma physics and the calculation of transport coefficients (conductivity, diffusivity, etc.), the fields generated by the sources and the motion of the sources are solved self-consistently. In such cases, however, the motion of a selected source is calculated in response to fields generated by all other sources. Rarely is the motion of a particle (source) due to the fields generated by that same particle calculated. The reason for this is twofold:
- Neglect of the "self-fieldsSelf-energyIn theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
" usually leads to answers that are accurate enough for many applications, and - Inclusion of self-fields leads to problems in physics such as renormalizationRenormalizationIn quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
, some of which still unsolved, that relate to the very nature of matter and energy.
This conceptual problems created by self-fields are highlighted in a standard graduate text. [Jackson]
The difficulties presented by this problem touch one of the most fundamental aspects of physics, the nature of the elementary particle. Although partial solutions, workable within limited areas, can be given, the basic problem remains unsolved. One might hope that the transition from classical to quantum-mechanical treatments would remove the difficulties. While there is still hope that this may eventually occur, the present quantum-mechanical discussions are beset with even more elaborate troubles than the classical ones. It is one of the triumphs of comparatively recent years (~ 1948 - 1950) that the concepts of Lorentz covariance and gauge invariance were exploited sufficiently cleverly to circumvent these difficulties in quantum electrodynamics and so allow the calculation of very small radiative effects to extremely high precision, in full agreement with experiment. From a fundamental point of view, however, the difficulties remain.
The magnetic radiation reaction force is the result of the most fundamental calculation of the effect of self-generated fields. It arises from the observation that accelerating non-relativistic particles with associated magnetic moment emit radiation. The Abraham–Lorentz force is the average force that an accelerating charged particle feels in the recoil from the emission of radiation. The introduction of quantum effects
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
leads one to quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
. The self-fields in quantum electrodynamics generate a finite number of infinities in the calculations that can be removed by the process of renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
. This has led to a theory that is able to make the most accurate predictions that humans have made to date. See precision tests of QED
Precision tests of QED
Quantum electrodynamics , a relativistic quantum field theory of electrodynamics, is among the most stringently tested theories in physics....
. The renormalization process fails, however, when applied to the gravitational force. The infinities in that case are infinite in number, which causes the failure of renormalization. Therefore general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
has unsolved self-field problems. String theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
is a current attempt to resolve these problems for all forces.
Derivation
We begin with the Larmor formulaLarmor formula
In physics, in the area of electrodynamics, the Larmor formula is used to calculate the total power radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J...
for radiation of the second derivative of a magnetic moment with respect to time:
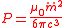.In the case that the magnetic moment is produced by an electric charge moving along a circular path is
-
,
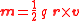where
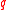is the position of the charge relative to the center of the circle and is the instantaneous velocity of the charge.The above Larmor formula
Larmor formula
In physics, in the area of electrodynamics, the Larmor formula is used to calculate the total power radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J...
becomes as follows:
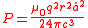.If we assume the motion of a charged particle is periodic, then the average work done on the particle by the Abraham–Lorentz force is the negative of the Larmor power integrated over one period from
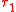to 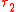: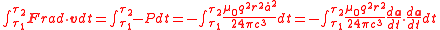.Notice that we can integrate the above expression by parts. If we assume that there is periodic motion, the boundary term in the integral by parts disappears:
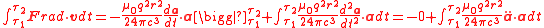.Integrating by parts a second time, we find
.Clearly, we can identify
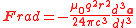.Signals from the future
Below is an illustration of how a classical analysis can lead to surprising results. The classical theory can be seen to challenge standard pictures of causality, thus signaling either a breakdown or a need for extension of the theory. In this case the extension is to quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and its relativistic counterpart quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. See the quote from Rohrlich in the introduction concerning "the importance of obeying the validity limits of a physical theory".
For a particle in an external force
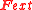, we have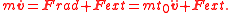where
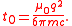
This equation can be integrated once to obtain
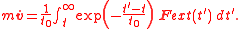
The integral extends from the present to infinitely far in the future. Thus future values of the force affect the acceleration of the particle in the present. The future values are weighted by the factor
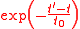
which falls off rapidly for times greater than
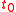in the future. Therefore, signals from an interval approximately 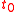into the future affect the acceleration in the present. For an electron, this time is approximately 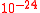sec, which is the time it takes for a light wave to travel across the "size" of an electron.See also
- Max AbrahamMax AbrahamMax Abraham was a German physicist.Abraham was born in Danzig, Imperial Germany to a family of Jewish merchants. His father was Moritz Abraham and his mother was Selma Moritzsohn. Attending the University of Berlin, he studied under Max Planck. He graduated in 1897...
- Hendrik LorentzHendrik LorentzHendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
- Cyclotron radiationCyclotron radiationCyclotron radiation is electromagnetic radiation emitted by moving charged particles deflected by a magnetic field. The Lorentz force on the particles acts perpendicular to both the magnetic field lines and the particles' motion through them, creating an acceleration of charged particles that...
- Electromagnetic massElectromagnetic massElectromagnetic mass was initially a concept of classical mechanics, denoting as to how much the electromagnetic field, or the self-energy, is contributing to the mass of charged particles. It was first derived by J. J. Thomson in 1881 and was for some time also considered as a dynamical...
- Radiation resistanceRadiation resistanceRadiation resistance is that part of an antenna's feedpoint resistance that is caused by the radiation of electromagnetic waves from the antenna. The radiation resistance is determined by the geometry of the antenna, not by the materials of which it is made...
- Radiation dampingRadiation dampingRadiation damping in accelerator physics is a way of reducing the beam emittance of a high-velocity beam of charged particles.There are two main ways of using radiation damping to reduce the emittance of a particle beam—damping rings and undulators—and both rely on the same principle...
- Synchrotron radiationSynchrotron radiationThe electromagnetic radiation emitted when charged particles are accelerated radially is called synchrotron radiation. It is produced in synchrotrons using bending magnets, undulators and/or wigglers...
- Wheeler–Feynman absorber theory
Further reading
See sections 11.2.2 and 11.2.3\- Jose A. Heras, The Radiation Force of an Electron Reexamined, 2003, http://www.joseheras.com/jheras_papers/JAH-PAPER_16.pdf.
- Donald H. Menzel, Fundamental Formulas of Physics, 1960, Dover Publications Inc., ISBN 0-486-60595-7, vol. 1, page 345.