
Margules activity model
Encyclopedia
Introduction
Max MargulesMax Margules
-Life and career:Max Margules studied mathematics, physics, and chemistry in Vienna. In 1877 he joined, as volunteer, ZAMG in Vienna . After two years he left Vienna to study 1 year at Berlin. He returned to Vienna and received his Phd degree in the area of Electrodynamics. During his doctoral...
introduced in 1895 a simple thermodynamic model for the excess Gibbs free energy of a liquid mixture.
After Lewis had introduced the concept of the activity coefficient, the model could be used to derive an expression for the activity coefficient
Activity coefficient
An activity coefficient is a factor used in thermodynamics to account for deviations from ideal behaviour in a mixture of chemical substances. In an ideal mixture, the interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed...
s
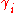
of a compound i in a liquid. The activity coefficient is a measure for the deviation from ideal solubility, also known as Raoult's law. In Chemical Engineering the Margules' Gibbs free energy model for liquid mixtures is better known as the Margules activity or activity coefficient model.
Although the model is old it has the characteristic feature to describe extrema in the activity coefficient, while modern models like UNIQUAC
UNIQUAC
UNIQUAC is an activity coefficient model used in description of phase equilibria.The model is a so-called lattice model and has been derived from a first order approximation...
, NRTL and Wilson
Wilson
- People :* Wilson * Woodrow Wilson , 28th President of the United States* Wilson Francisco Alves , often only Wilson, Brazilian footballer of Brazil and Vasco da Gama* Harold Wilson, UK Prime Minister 1964-70, 1974-6...
can not.
Excess Gibbs free energy
Margules expressed the excess Gibbs free energy of a binary liquid mixture as a power series of the mole fractions xi: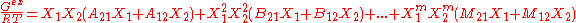
In here the A, B are constants, which are derived from regressing experimental phase equilibria data.
Frequently the B and higher order parameters are set to zero. The leading term
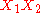 assures that the excess Gibbs energy becomes zero at x1=0 and x1=1.
assures that the excess Gibbs energy becomes zero at x1=0 and x1=1.Activity coefficient
The activity coefficient of component i is found by differentiation of the excess Gibbs energy towards xi.This yields, when applied only to the first term and using the Gibbs-Duhem equation, :
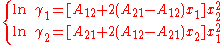
In here A12 and A21 are constants which are equal to the logarithm of the limiting activity coefficients:
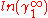 and
and 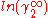 respectively.
respectively.When
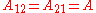 , which implies molecules of same molecular size but different polarity, the equations reduce to the one-parameter Margules activity model:
, which implies molecules of same molecular size but different polarity, the equations reduce to the one-parameter Margules activity model: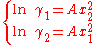
In that case the activity coefficients cross at x1=0.5 and the limiting activity coefficients are equal. When A=0 the model reduces to the ideal solution, i.e. the activity of a compound equals to its concentration (mole fraction).
Extrema
When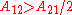 the activity coefficient curves are monotonic increasing
the activity coefficient curves are monotonic increasing 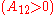 or decreasing
or decreasing 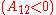 , and have the extrema at x1=0 .
, and have the extrema at x1=0 .When
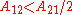 the activity coefficient curve of component 1 shows a maximum and compound 2 minimum at:
the activity coefficient curve of component 1 shows a maximum and compound 2 minimum at: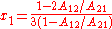
It is easily seen that when A12=0 and A21>0 that a maximum in the activity coefficient of compound 1 exists at x1=1/3. Obvious, the activity coefficient of compound 2 goes at this concentration through a minimum as a result of the Gibbs-Duhem rule.
The binary system Chloroform-Methanol is an example of a system that shows a maximum in the activity coefficient, i.c. Chloroform. The parameters for a description at 20°C are A12=0.6298 and A21=1.9522. This gives a maximum in the activity of Chloroform at x1=0.17.
In general, for the case A=A12=A21, the larger parameter A, the more the binary systems deviates from Raoult's law; i.e. ideal solubility. When A>2 the system starts to demix in two liquids at 50/50 composition; i.e. plait point is at 50 mol%. Since:
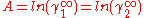

For assymetric binary systems, A12≠A21, the liquid-liquid separation always occurs for
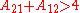
Or equivalent:

The plait point is not located at 50 mol%. It depends from the ratio in limiting activity coefficients.

