
Mass–luminosity relation
Encyclopedia
In astrophysics
, the mass–luminosity relation is an equation giving the relationship between a star's mass and its luminosity
. The relationship is represented by the equation: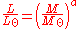
where L⊙ and M⊙ are the luminosity and mass of the sun and 1 < a < 6. The value a = 3.5 is commonly used for main-sequence stars. This equation and the usual value of a = 3.5 only applies to main-sequence stars with masses 2M⊙ < M < 20M⊙ and does not apply to red giants or white dwarfs.
In summary, the relations for stars with different ranges of mass are to good approximation the following:
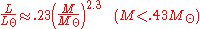
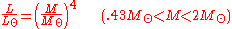
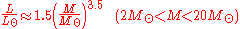
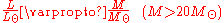
For stars with masses less than .43M⊙, convection
is the sole energy transport process, so the relation changes significantly. For stars with masses M > 20M⊙ the relationship flattens out and becomes L ∝ M. It can be shown this change is due to an increase in radiation pressure
in massive stars. These equations are determined empirically by determining the mass of stars in binary systems to which the distance is known via standard parallax measurements or other techniques. After enough stars are plotted, stars will form a line on a logarithmic plot and slope of the line gives the proper value of a.
The mass–luminosity relation is important because it can be used to find the distance to binary system
s which are too far for normal parallax
measurements, using a technique called "dynamical parallax
". In this technique, the masses of the two stars in a binary system are estimated, usually as being the mass of the sun. Then, using Kepler's laws of celestial mechanics
, the distance between the stars is calculated. Once this distance is found, the distance away can be found via the arc subtended in the sky, giving a preliminary distance measurement. From this measurement and the apparent magnitude
s of both stars, the luminosities can be found, and by using the mass–luminosity relationship, the masses of each star. These masses are used to re-calculate the separation distance, and the process is repeated. The process is iterated many times, and accuracies as high as 5% can be achieved. The mass–luminosity relationship can also be used to determine the lifetime of stars by noting that lifetime is approximately proportional to M/L. One finds that more massive stars live shorter. A more sophisticated calculation factors in a star's loss of mass over time.
To the first approximation, stars are black body
radiators with a surface area of 4πR2. Thus, from the Stefan-Boltzmann law we find that the luminosity (energy emitted per second) is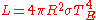
Where σ is Stefan's constant, 5.67 × 10−8W m−2 K−4.
Under the condition of hydrostatic equilibrium
,
By integrating both sides of this relation from r = 0 to r = R, one arrives at a form of the virial theorem: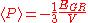
The potential energy
of a spherical mass distribution is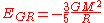 . This and the volume are substituted in to give:
. This and the volume are substituted in to give:
Simplifying greatly, we next use the ideal gas law
(PV = nkT) to solve for the temperature.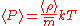
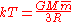 .
.
Here is the average mass of gas particles within the star. Now, we can substitute this equation into the initial luminosity equation, along with
is the average mass of gas particles within the star. Now, we can substitute this equation into the initial luminosity equation, along with to arrive at
to arrive at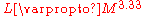
A slightly more exact result can be achieved by considering that the above equation gives the average temperature based on the average pressure, but what is actually needed is the surface temperature. Because stars are much hotter in the center then near the surface, we next need to estimate the relationship between the surface temperature and internal temperature. The center is so much hotter since energy takes a long time to escape, otherwise, thermodynamic equilibrium would be achieved quickly and the temperature would be nearly uniform throughout. We can use a random walk
analysis to estimate the "delay factor", ie. the amount of time it takes energy to escape. We let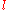 represent the mean free path
represent the mean free path
for a photon within the sun. In actuality, the mean free path depends on the density and temperature, but here it will be approximated as a constant. After N interactions, resulting in N vector displacements in random directions, the distance traveled is:
The square of the net displacement is: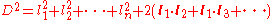
If we average over many random direction changes, the terms involving dot products cancel because the direction is random. Hence, for large ,
,
Thus, to escape from the sun, on average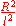 steps are required. The time this takes is
steps are required. The time this takes is 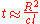 . In contrast, the time to escape directly out of the sun from the center is
. In contrast, the time to escape directly out of the sun from the center is  , which is a factor of
, which is a factor of  shorter.
shorter.
Thus, factoring this into the Stefan-Boltzmann law, we find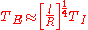 .
.
Thus, combining the above equations, we find that
But the mean free path
is inversely proportional to the product of the cross section and the numerical density, and thus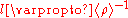
which gives
 and to consider the internal temperature TI directly; more precisely, we consider the average temperature in the radiation zone
and to consider the internal temperature TI directly; more precisely, we consider the average temperature in the radiation zone
.
We begin by noting a relation between the radiation pressure
Prad and luminosity. The gradient of radiation pressure is equal to the momentum transfer absorbed from the radiation, giving:
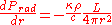
where c is the velocity of light. Note that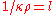 , the photon mean free path.
, the photon mean free path.
The radiation pressure is related to the temperature by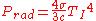 , so we have
, so we have
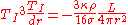
from which it follows directly that
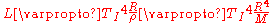 .
.
In the radiation zone gravity is balanced by the pressure on the gas coming from both itself (approxiamted by ideal gas pressure) and from the radiation. For a small enough stellar mass the latter is negligible and one arrives at
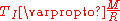
as before. More precisely, since we integrated from 0 to R we have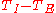 on the left side, but we may neglect the surface temperature TE with respect to the internal temperature TI.
on the left side, but we may neglect the surface temperature TE with respect to the internal temperature TI.
From this it follows directly that

For a large enough stellar mass, the radiation pressure is larger than the gas pressure in the radiation zone. Plugging the radiation pressure instead of the ideal gas pressure we used above, we get:

hence

Astrophysics
Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...
, the mass–luminosity relation is an equation giving the relationship between a star's mass and its luminosity
Luminosity
Luminosity is a measurement of brightness.-In photometry and color imaging:In photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre.The luminosity function...
. The relationship is represented by the equation:
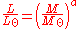
where L⊙ and M⊙ are the luminosity and mass of the sun and 1 < a < 6. The value a = 3.5 is commonly used for main-sequence stars. This equation and the usual value of a = 3.5 only applies to main-sequence stars with masses 2M⊙ < M < 20M⊙ and does not apply to red giants or white dwarfs.
In summary, the relations for stars with different ranges of mass are to good approximation the following:
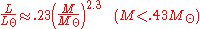
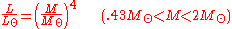
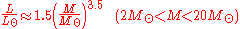
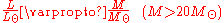
For stars with masses less than .43M⊙, convection
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
is the sole energy transport process, so the relation changes significantly. For stars with masses M > 20M⊙ the relationship flattens out and becomes L ∝ M. It can be shown this change is due to an increase in radiation pressure
Radiation pressure
Radiation pressure is the pressure exerted upon any surface exposed to electromagnetic radiation. If absorbed, the pressure is the power flux density divided by the speed of light...
in massive stars. These equations are determined empirically by determining the mass of stars in binary systems to which the distance is known via standard parallax measurements or other techniques. After enough stars are plotted, stars will form a line on a logarithmic plot and slope of the line gives the proper value of a.
The mass–luminosity relation is important because it can be used to find the distance to binary system
Binary system (astronomy)
A binary system is an astronomical term referring to two objects in space which are so close that their gravitational interaction causes them to orbit about a common center of mass. Some definitions A binary system is an astronomical term referring to two objects in space (usually stars, but also...
s which are too far for normal parallax
Parallax
Parallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines. The term is derived from the Greek παράλλαξις , meaning "alteration"...
measurements, using a technique called "dynamical parallax
Dynamical Parallax
In astronomy, the distance to a visual binary star may be estimated from the masses of its two components, the size of their orbit, and the period of their revolution around one another...
". In this technique, the masses of the two stars in a binary system are estimated, usually as being the mass of the sun. Then, using Kepler's laws of celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, the distance between the stars is calculated. Once this distance is found, the distance away can be found via the arc subtended in the sky, giving a preliminary distance measurement. From this measurement and the apparent magnitude
Apparent magnitude
The apparent magnitude of a celestial body is a measure of its brightness as seen by an observer on Earth, adjusted to the value it would have in the absence of the atmosphere...
s of both stars, the luminosities can be found, and by using the mass–luminosity relationship, the masses of each star. These masses are used to re-calculate the separation distance, and the process is repeated. The process is iterated many times, and accuracies as high as 5% can be achieved. The mass–luminosity relationship can also be used to determine the lifetime of stars by noting that lifetime is approximately proportional to M/L. One finds that more massive stars live shorter. A more sophisticated calculation factors in a star's loss of mass over time.
Derivation
Deriving a theoretically exact mass–luminosity relation requires finding the energy generation equation and building a thermodynamic model of the inside of a star. However, the basic relation L ∝ M3 can be derived using some basic physics and simplifying assumptions. The first such derivation was performed by astrophysicist Arthur Eddington in 1924. The derivation showed that stars can be approximately modelled as ideal gasses, which was a new, somewhat radical idea at the time. What follows is very similar to Eddington's approach, but uses a random-walk analysis and does not include the optical opacity.To the first approximation, stars are black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
radiators with a surface area of 4πR2. Thus, from the Stefan-Boltzmann law we find that the luminosity (energy emitted per second) is
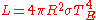
Where σ is Stefan's constant, 5.67 × 10−8W m−2 K−4.
Under the condition of hydrostatic equilibrium
Hydrostatic equilibrium
Hydrostatic equilibrium or hydrostatic balance is the condition in fluid mechanics where a volume of a fluid is at rest or at constant velocity. This occurs when compression due to gravity is balanced by a pressure gradient force...
,

By integrating both sides of this relation from r = 0 to r = R, one arrives at a form of the virial theorem:
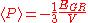
The potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
of a spherical mass distribution is
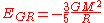 . This and the volume are substituted in to give:
. This and the volume are substituted in to give:
Simplifying greatly, we next use the ideal gas law
Ideal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
(PV = nkT) to solve for the temperature.
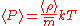
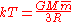 .
.Here
 is the average mass of gas particles within the star. Now, we can substitute this equation into the initial luminosity equation, along with
is the average mass of gas particles within the star. Now, we can substitute this equation into the initial luminosity equation, along with to arrive at
to arrive at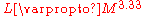
A slightly more exact result can be achieved by considering that the above equation gives the average temperature based on the average pressure, but what is actually needed is the surface temperature. Because stars are much hotter in the center then near the surface, we next need to estimate the relationship between the surface temperature and internal temperature. The center is so much hotter since energy takes a long time to escape, otherwise, thermodynamic equilibrium would be achieved quickly and the temperature would be nearly uniform throughout. We can use a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
analysis to estimate the "delay factor", ie. the amount of time it takes energy to escape. We let
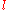 represent the mean free path
represent the mean free pathMean free path
In physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:...
for a photon within the sun. In actuality, the mean free path depends on the density and temperature, but here it will be approximated as a constant. After N interactions, resulting in N vector displacements in random directions, the distance traveled is:

The square of the net displacement is:
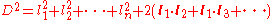
If we average over many random direction changes, the terms involving dot products cancel because the direction is random. Hence, for large
 ,
,
Thus, to escape from the sun, on average
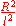 steps are required. The time this takes is
steps are required. The time this takes is 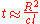 . In contrast, the time to escape directly out of the sun from the center is
. In contrast, the time to escape directly out of the sun from the center is  , which is a factor of
, which is a factor of  shorter.
shorter.Thus, factoring this into the Stefan-Boltzmann law, we find
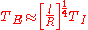 .
.Thus, combining the above equations, we find that

But the mean free path
Mean free path
In physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:...
is inversely proportional to the product of the cross section and the numerical density, and thus
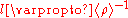
which gives

Distinguishing between small and large stellar masses
One may distinguish between the cases of small and large stellar masses by deriving the above results using radiation pressure. In this case, it is easier to use the optical opacity and to consider the internal temperature TI directly; more precisely, we consider the average temperature in the radiation zone
and to consider the internal temperature TI directly; more precisely, we consider the average temperature in the radiation zoneRadiation zone
The radiation zone is the middle zone in the Sun's interior. Energy travels out of the core into the radiation zone. Energy that travels through the radiation zone is in the form of electromagnetic radiation. The radiation zone is so dense that the waves bounce around...
.
We begin by noting a relation between the radiation pressure
Radiation pressure
Radiation pressure is the pressure exerted upon any surface exposed to electromagnetic radiation. If absorbed, the pressure is the power flux density divided by the speed of light...
Prad and luminosity. The gradient of radiation pressure is equal to the momentum transfer absorbed from the radiation, giving:
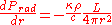
where c is the velocity of light. Note that
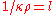 , the photon mean free path.
, the photon mean free path.The radiation pressure is related to the temperature by
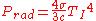 , so we have
, so we have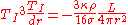
from which it follows directly that
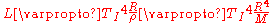 .
.In the radiation zone gravity is balanced by the pressure on the gas coming from both itself (approxiamted by ideal gas pressure) and from the radiation. For a small enough stellar mass the latter is negligible and one arrives at
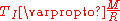
as before. More precisely, since we integrated from 0 to R we have
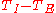 on the left side, but we may neglect the surface temperature TE with respect to the internal temperature TI.
on the left side, but we may neglect the surface temperature TE with respect to the internal temperature TI.From this it follows directly that

For a large enough stellar mass, the radiation pressure is larger than the gas pressure in the radiation zone. Plugging the radiation pressure instead of the ideal gas pressure we used above, we get:

hence


