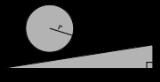
Measurement of a Circle
Encyclopedia
Measurement of a Circle is a treatise
that consists of three propositions by Archimedes
. The treatise is only a fraction of what was a longer work.
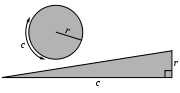Proposition one states:
Any circle
with a circumference
c and a radius
r is equal in area
with a right triangle
with the two legs
being c and r. This proposition is proved by the method of exhaustion
.
This proposition could not have been placed by Archimedes, for it relies on the outcome of the third proposition.
Proposition three states:
This approximates what we now call the mathematical constant
π. He found these bounds on the value of π by inscribing
and circumscribing a circle with two similar
96-sided regular polygon
s.
(one larger and one smaller) and other larger non-perfect square root
s; however, Archimedes gives no explanation as to how he found these numbers.
He gives the upper and lower bounds to √3 as
However, these bounds are familiar from the
study of Pell's equation
and the convergents of an associated continued fraction
, leading to much speculation as to
how much of this number theory might have been accessible to Archimedes. Discussion of this approach goes back at least to
Thomas Fantet de Lagny, FRS (compare Chronology of computation of π) in 1723, but was treated more explicitly by
Hieronymus Georg Zeuthen
. In the early 1880s, Friedrich Otto Hultsch (1833--1906) and Karl Heinrich Hunrath
(b. 1847) noted how the bounds could be found quickly by means of simple binomial bounds on square roots close to a perfect
square modelled on Elements II.4, 7; this method is favoured by Heath. Although only one route to the bounds is mentioned,
in fact there are two others, making the bounds almost inescapable however the method is worked. But the bounds can also be produced by an iterative geometrical construction suggested by Archimedes' Stomachion in the setting of the regular
dodecagon. In this case, the task is to give rational approximations to the tangent of π/12.
Treatise
A treatise is a formal and systematic written discourse on some subject, generally longer and treating it in greater depth than an essay, and more concerned with investigating or exposing the principles of the subject.-Noteworthy treatises:...
that consists of three propositions by Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
. The treatise is only a fraction of what was a longer work.
Proposition one
The area of any circle is equal to a right-angled triangle in which one of the sides about the right angle is equal to the radius, and the other to the circumference, of the circle.
Any circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
with a circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
c and a radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
r is equal in area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
with a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
with the two legs
Cathetus
In a right triangle, the cathetus , commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called the periphrasis . The side opposite the right angle is the hypotenuse...
being c and r. This proposition is proved by the method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
.
Proposition two
Proposition two states:The area of a circle is to the square on its diameter as 11 to 14.
This proposition could not have been placed by Archimedes, for it relies on the outcome of the third proposition.
Proposition three
The ratio of the circumference of any circle to its diameter is greater thanbut less than
.
This approximates what we now call the mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
π. He found these bounds on the value of π by inscribing
Inscribe
right|thumb|An inscribed triangle of a circleIn geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "Figure F is inscribed in figure G" means precisely the same thing as "figure G is circumscribed about...
and circumscribing a circle with two similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
96-sided regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s.
Approximation to square roots
This proposition also contains accurate approximations to the square root of 3Square root of 3
The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is more precisely called the principal square root of 3, to distinguish it from the negative number with the same property...
(one larger and one smaller) and other larger non-perfect square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s; however, Archimedes gives no explanation as to how he found these numbers.
He gives the upper and lower bounds to √3 as
However, these bounds are familiar from thestudy of Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
and the convergents of an associated continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
, leading to much speculation as to
how much of this number theory might have been accessible to Archimedes. Discussion of this approach goes back at least to
Thomas Fantet de Lagny, FRS (compare Chronology of computation of π) in 1723, but was treated more explicitly by
Hieronymus Georg Zeuthen
Hieronymus Georg Zeuthen
Hieronymus Georg Zeuthen was a Danish mathematician.He is known for work on the enumerative geometry of conic sections, algebraic surfaces, and history of mathematics.-Biography:...
. In the early 1880s, Friedrich Otto Hultsch (1833--1906) and Karl Heinrich Hunrath
(b. 1847) noted how the bounds could be found quickly by means of simple binomial bounds on square roots close to a perfect
square modelled on Elements II.4, 7; this method is favoured by Heath. Although only one route to the bounds is mentioned,
in fact there are two others, making the bounds almost inescapable however the method is worked. But the bounds can also be produced by an iterative geometrical construction suggested by Archimedes' Stomachion in the setting of the regular
dodecagon. In this case, the task is to give rational approximations to the tangent of π/12.