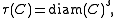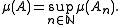Metric outer measure
Encyclopedia
In mathematics
, a metric outer measure is an outer measure
μ defined on the subset
s of a given metric space
(X, d) such that
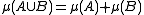
for every pair of positively separated subsets A and B of X.
on X, i.e. a set function defined on a class Σ of subsets of X containing the empty set ∅, such that τ(∅) = 0. One can show that the set function μ defined by
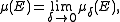
where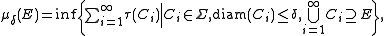
is not only an outer measure, but in fact a metric outer measure as well. (Some authors prefer to take a supremum
over δ > 0 rather than a limit
as δ → 0; the two give the same result, since μδ(E) increases as δ decreases.)
For the function τ one can use
where s is a positive constant; this τ is defined on the power set of all subsets of X; the associated measure μ is the s-dimensional Hausdorff measure
. More generally, one could use any so-called dimension function
.
This construction is very important in fractal geometry, since this is how the Hausdorff and packing measures are obtained.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a metric outer measure is an outer measure
Outer measure
In mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by...
μ defined on the subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of a given metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(X, d) such that
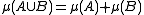
for every pair of positively separated subsets A and B of X.
Construction of metric outer measures
Let τ : Σ → [0, +∞] be a pre-measurePre-measure
In mathematics, a pre-measure is a function that is, in some sense, a precursor to a bona fide measure on a given space. Pre-measures are particularly useful in fractal geometry and dimension theory, where they can be used to define measures such as Hausdorff measure and packing measure on metric...
on X, i.e. a set function defined on a class Σ of subsets of X containing the empty set ∅, such that τ(∅) = 0. One can show that the set function μ defined by
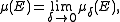
where
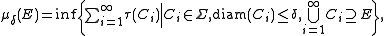
is not only an outer measure, but in fact a metric outer measure as well. (Some authors prefer to take a supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
over δ > 0 rather than a limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
as δ → 0; the two give the same result, since μδ(E) increases as δ decreases.)
For the function τ one can use
where s is a positive constant; this τ is defined on the power set of all subsets of X; the associated measure μ is the s-dimensional Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
. More generally, one could use any so-called dimension function
Dimension function
In mathematics, the notion of an dimension function is a tool in the study of fractals and other subsets of metric spaces...
.
This construction is very important in fractal geometry, since this is how the Hausdorff and packing measures are obtained.
Properties of metric outer measures
Let μ be a metric outer measure on a metric space (X, d).- For any sequence of subsets An, n ∈ N, of X with
- and such that An and A \ An+1 are positively separated, it follows that
- All the d-closed subsetsClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
E of X are μ-measurable in the sense that they satisfy the following version of Carathéodory's criterion: for all sets A and B with A ⊆ E and B ⊆ X \ E,
- Consequently, all the Borel subsets of X — those obtainable as countable unions, intersections and set-theoretic differences of open/closed sets — are μ-measurable.