Model predictive control
Encyclopedia
Model Predictive Control, or MPC, is an advanced method of process control
that has been in use in the process
industries such as chemical plant
s and oil refineries since the 1980s. Model predictive controllers rely on dynamic models of the process, most often linear empirical
models obtained by system identification
.
s. The additional complexity of the MPC control algorithm is not generally needed to provide adequate control of simple systems, which are often controlled well by generic PID controller
s. Common dynamic characteristics that are difficult for PID controllers include large time delays and high-order dynamics.
MPC models predict the change in the dependent variables of the modeled system that will be caused by changes in the independent variable
s. In a chemical process, independent variables that can be adjusted by the controller are often either the setpoints of regulatory PID controllers (pressure, flow, temperature, etc.) or the final control element (valves, dampers, etc.). Independent variables that cannot be adjusted by the controller are used as disturbances. Dependent variables in these processes are other measurements that represent either control objectives or process constraints.
MPC uses the current plant measurements, the current dynamic state of the process, the MPC models, and the process variable targets and limits to calculate future changes in the independent variables. These changes are calculated to hold the dependent variables close to target while honoring constraints on both independent and dependent variables. The MPC typically sends out only the first change in each independent variable to be implemented, and repeats the calculation when the next change is required.
While many real processes are not linear, they can often be considered to be approximately linear over a small operating range. Linear MPC approaches are used in the majority of applications with the feedback mechanism of the MPC compensating for prediction errors due to structural mismatch between the model and the process. In model predictive controllers that consist only of linear models, the superposition principle
of linear algebra
enables the effect of changes in multiple independent variables to be added together to predict the response of the dependent variables. This simplifies the control problem to a series of direct matrix algebra calculations that are fast and robust.
When linear models are not sufficiently accurate to represent the real process nonlinearities, several approaches can be used. In some cases, the process variables can be transformed before and/or after the linear MPC model to reduce the nonlinearity. The process can be controlled with nonlinear MPC that uses a nonlinear model directly in the control application. The nonlinear model may be in the form of an empirical data fit (e.g. artificial neural networks) or a high-fidelity dynamic model based on fundamental mass and energy balances. The nonlinear model may be linearized to derive a Kalman filter
or specify a model for linear MPC.
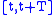. Specifically, an online or on-the-fly calculation is used to explore state trajectories that emanate from the current state and find (via the solution of Euler-Lagrange equation
s) a cost-minimizing control strategy until time
. Only the first step of the control strategy is implemented, then the plant state is sampled again and the calculations are repeated starting from the now current state, yielding a new control and new predicted state path. The prediction horizon keeps being shifted forward and for this reason MPC is also called receding horizon control. Although this approach is not optimal, in practice it has given very good results. Much academic research has been done to find fast methods of solution of Euler-Lagrange type equations, to understand the global stability properties of MPC's local optimization, and in general to improve the MPC method. To some extent the theoreticians have been trying to catch up with the control engineers when it comes to MPC.
to calculate the optimum control moves.
The optimization cost function is given by:
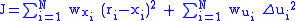
without violating constraints (low/high limits)
With:
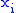= i -th controlled variable (e.g. measured temperature)
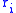= i -th reference variable (e.g. required temperature)
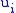= i -th manipulated variable (e.g. control valve)
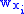= weighting coefficient reflecting the relative importance of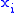 
= weighting coefficient penalizing relative big changes in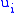 
etc.
The numerical solution of the NMPC optimal control problems is typically based on direct optimal control methods using Newton-type optimization schemes, in one of the variants: direct single shooting
, direct multiple shooting method
s, or direct collocation
. NMPC algorithms typically exploit the fact that consecutive optimal control problems are similar to each other.
This allows to initialize the Newton-type solution procedure efficiently by a suitably shifted guess from the previously computed optimal solution, saving considerable amounts of computation time. The similarity of subsequent problems is even further exploited by path following algorithms (or "real-time iterations") that never attempt to iterate any optimization problem to convergence, but instead only take one iteration towards the solution of the most current NMPC problem, before proceeding to the next one, which is suitably initialized.
While NMPC applications have in the past been mostly used in the process and chemical industries with comparatively slow sampling rates, NMPC is more and more being applied to applications with high sampling rates, e.g., in the automotive industry.
A survey of commercially available packages has been provided by S.J. Qin and T.A. Badgwell in Control Engineering Practice 11 (2003) 733–764 http://www.scribd.com/doc/16955545/MPC-CEP-Qin-Badgwell.
Process control
Process control is a statistics and engineering discipline that deals with architectures, mechanisms and algorithms for maintaining the output of a specific process within a desired range...
that has been in use in the process
Industrial process
Industrial processes are procedures involving chemical or mechanical steps to aid in the manufacture of an item or items, usually carried out on a very large scale. Industrial processes are the key components of heavy industry....
industries such as chemical plant
Chemical plant
A chemical plant is an industrial process plant that manufactures chemicals, usually on a large scale. The general objective of a chemical plant is to create new material wealth via the chemical or biological transformation and or separation of materials. Chemical plants use special equipment,...
s and oil refineries since the 1980s. Model predictive controllers rely on dynamic models of the process, most often linear empirical
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
models obtained by system identification
System identification
In control engineering, the field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data...
.
Overview
The models used in MPC are generally intended to represent the behavior of complex dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s. The additional complexity of the MPC control algorithm is not generally needed to provide adequate control of simple systems, which are often controlled well by generic PID controller
PID controller
A proportional–integral–derivative controller is a generic control loop feedback mechanism widely used in industrial control systems – a PID is the most commonly used feedback controller. A PID controller calculates an "error" value as the difference between a measured process variable and a...
s. Common dynamic characteristics that are difficult for PID controllers include large time delays and high-order dynamics.
MPC models predict the change in the dependent variables of the modeled system that will be caused by changes in the independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s. In a chemical process, independent variables that can be adjusted by the controller are often either the setpoints of regulatory PID controllers (pressure, flow, temperature, etc.) or the final control element (valves, dampers, etc.). Independent variables that cannot be adjusted by the controller are used as disturbances. Dependent variables in these processes are other measurements that represent either control objectives or process constraints.
MPC uses the current plant measurements, the current dynamic state of the process, the MPC models, and the process variable targets and limits to calculate future changes in the independent variables. These changes are calculated to hold the dependent variables close to target while honoring constraints on both independent and dependent variables. The MPC typically sends out only the first change in each independent variable to be implemented, and repeats the calculation when the next change is required.
While many real processes are not linear, they can often be considered to be approximately linear over a small operating range. Linear MPC approaches are used in the majority of applications with the feedback mechanism of the MPC compensating for prediction errors due to structural mismatch between the model and the process. In model predictive controllers that consist only of linear models, the superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
enables the effect of changes in multiple independent variables to be added together to predict the response of the dependent variables. This simplifies the control problem to a series of direct matrix algebra calculations that are fast and robust.
When linear models are not sufficiently accurate to represent the real process nonlinearities, several approaches can be used. In some cases, the process variables can be transformed before and/or after the linear MPC model to reduce the nonlinearity. The process can be controlled with nonlinear MPC that uses a nonlinear model directly in the control application. The nonlinear model may be in the form of an empirical data fit (e.g. artificial neural networks) or a high-fidelity dynamic model based on fundamental mass and energy balances. The nonlinear model may be linearized to derive a Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
or specify a model for linear MPC.
Theory behind MPC
MPC is based on iterative, finite horizon optimization of a plant model. At time the current plant state is sampled and a cost minimizing control strategy is computed (via a numerical minimization algorithm) for a relatively short time horizon in the future: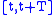. Specifically, an online or on-the-fly calculation is used to explore state trajectories that emanate from the current state and find (via the solution of Euler-Lagrange equationEuler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
s) a cost-minimizing control strategy until time
. Only the first step of the control strategy is implemented, then the plant state is sampled again and the calculations are repeated starting from the now current state, yielding a new control and new predicted state path. The prediction horizon keeps being shifted forward and for this reason MPC is also called receding horizon control. Although this approach is not optimal, in practice it has given very good results. Much academic research has been done to find fast methods of solution of Euler-Lagrange type equations, to understand the global stability properties of MPC's local optimization, and in general to improve the MPC method. To some extent the theoreticians have been trying to catch up with the control engineers when it comes to MPC.Principles of MPC
Model Predictive Control (MPC) is a multivariable control algorithm that uses:- an internal dynamic model of the process
- a history of past control moves and
- an optimization cost function J over the receding prediction horizon,
to calculate the optimum control moves.
The optimization cost function is given by:
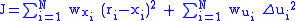
without violating constraints (low/high limits)
With:
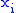= i -th controlled variable (e.g. measured temperature) 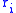= i -th reference variable (e.g. required temperature) 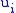= i -th manipulated variable (e.g. control valve) 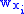= weighting coefficient reflecting the relative importance of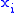 = weighting coefficient penalizing relative big changes in 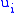etc.
Nonlinear MPC
Nonlinear Model Predictive Control, or NMPC, is a variant of model predictive control (MPC) that is characterized by the use of nonlinear system models in the prediction. As in linear MPC, NMPC requires the iterative solution of optimal control problems on a finite prediction horizon. While these problems are convex in linear MPC, in nonlinear MPC they are not convex anymore. This poses challenges for both, NMPC stability theory and numerical solution.The numerical solution of the NMPC optimal control problems is typically based on direct optimal control methods using Newton-type optimization schemes, in one of the variants: direct single shooting
Shooting method
In numerical analysis, the shooting method is a method for solving a boundary value problem by reducing it to the solution of an initial value problem...
, direct multiple shooting method
Direct multiple shooting method
In the area of mathematics known as numerical ordinary differential equations, the direct multiple shooting method is a numerical method for the solution of boundary value problems...
s, or direct collocation
Collocation method
In mathematics, a collocation method is a method for the numerical solution of ordinary differential equations, partial differential equations and integral equations...
. NMPC algorithms typically exploit the fact that consecutive optimal control problems are similar to each other.
This allows to initialize the Newton-type solution procedure efficiently by a suitably shifted guess from the previously computed optimal solution, saving considerable amounts of computation time. The similarity of subsequent problems is even further exploited by path following algorithms (or "real-time iterations") that never attempt to iterate any optimization problem to convergence, but instead only take one iteration towards the solution of the most current NMPC problem, before proceeding to the next one, which is suitably initialized.
While NMPC applications have in the past been mostly used in the process and chemical industries with comparatively slow sampling rates, NMPC is more and more being applied to applications with high sampling rates, e.g., in the automotive industry.
Commercially available MPC software
Commercial MPC packages are available and typically contain tools for model identification and analysis, controller design and tuning, as well as controller performance evaluation.A survey of commercially available packages has been provided by S.J. Qin and T.A. Badgwell in Control Engineering Practice 11 (2003) 733–764 http://www.scribd.com/doc/16955545/MPC-CEP-Qin-Badgwell.
See also
- System identificationSystem identificationIn control engineering, the field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data...
- Control theoryControl theoryControl theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
- Control engineeringControl engineeringControl engineering or Control systems engineering is the engineering discipline that applies control theory to design systems with predictable behaviors...
- Feed-forwardFeed-forwardFeed-forward is a term describing an element or pathway within a control system which passes a controlling signal from a source in the control system's external environment, often a command signal from an external operator, to a load elsewhere in its external environment...
External links
- Control Tuning and Best Practices
- M. Nikolaou: Model Predictive Controllers
- P. Orukpe: Basics of Model Predictive Control
- Case Study. Lancaster Waste Water Treatment Works, optimisation by means of Model Predictive Control from Perceptive Engineering
- ACADO Toolkit - Open Source Toolkit for Automatic Control and Dynamic Optimization providing linear and non-linear MPC tools. (C++, MATLAB interface available)
- Model Predictive Control Free book edited by Tao Zheng, Publisher: Sciyo, 2010.