
Morava K-theory
Encyclopedia
In stable homotopy theory
, a branch of mathematics
, Morava K-theory is one of a collection of cohomology theories introduced in algebraic topology
by Jack Morava
in unpublished preprints in the early 1970s. For every prime number
p (which is suppressed in the notation), it consists of theories K(n) for each nonnegative integer n, each a ring spectrum
in the sense of homotopy theory. published the first account of the theories.
with rational coefficients, whereas K(1) is a summand of mod-p complex K-theory. The theory K(n) has coefficient ring
where vn has degree 2(pn − 1). In particular, Morava K-theory is periodic with this period, in much the same way that complex K-theory has period 2.
These theories have several remarkable properties.
Stable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Morava K-theory is one of a collection of cohomology theories introduced in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
by Jack Morava
Jack Morava
Jack Johnson Morava is an American topologist.Of Czech and Appalachian descent, he was raised in Mercedes, Texas ; an early interest in topology was strongly encouraged by his parents...
in unpublished preprints in the early 1970s. For every prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p (which is suppressed in the notation), it consists of theories K(n) for each nonnegative integer n, each a ring spectrum
Ring spectrum (homotopy theory)
In stable homotopy theory, a ring spectrum is a spectrum E together with a multiplication mapand a unit mapwhere S is the sphere spectrum. These maps have to satisfy associativity and unitality conditions up to homotopy much in the same way as the multiplication of a ring is associative and unital...
in the sense of homotopy theory. published the first account of the theories.
Details
The theory K(0) agrees with singular homologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
with rational coefficients, whereas K(1) is a summand of mod-p complex K-theory. The theory K(n) has coefficient ring
- Fp[vn,vn−1]
where vn has degree 2(pn − 1). In particular, Morava K-theory is periodic with this period, in much the same way that complex K-theory has period 2.
These theories have several remarkable properties.
- They have Künneth isomorphismsKünneth theoremIn mathematics, especially in homological algebra and algebraic topology, a Künneth theorem is a statement relating the homology of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology of two topological spaces X and Y and their...
for arbitrary pairs of spaces: that is, for X and Y CW complexes, we have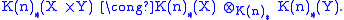
- They are "fields" in the categoryCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of ring spectraRing spectrum (homotopy theory)In stable homotopy theory, a ring spectrum is a spectrum E together with a multiplication mapand a unit mapwhere S is the sphere spectrum. These maps have to satisfy associativity and unitality conditions up to homotopy much in the same way as the multiplication of a ring is associative and unital...
. In other words every module spectrum over K(n) is free, i.e. a wedgeWedge sumIn topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
of suspensions of K(n). - They are complex orientedComplex cobordismIn mathematics, complex cobordism is a generalized cohomology theory related to cobordism of manifolds. Its spectrum is denoted by MU. It is an exceptionally powerful cohomology theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories...
, and the formal groupFormal groupIn mathematics, a formal group law is a formal power series behaving as if it were the product of a Lie group. They were introduced by . The term formal group sometimes means the same as formal group law, and sometimes means one of several generalizations. Formal groups are intermediate between...
they define has height n. - Every finite p-local spectrumSpectrum (homotopy theory)In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
X has the property that K(n)∗(X) = 0 if and only if n is less than a certain number N, called the typeTypeType may refer to:In philosophy:*Type–token distinctionIn mathematics:*Type *Type theory, basis for the study of type systems*Type or arity, the number of operands a function takes...
of the spectrum X. By a theorem of Devinatz–Hopkins–Smith, every thick subcategory of the categoryCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of finite p-local spectra is the subcategory of type-n spectra for some n.

