Movable singularity
Encyclopedia
In the theory of ordinary differential equation
s, a movable singularity is a point where the solution of the equation behaves badly
and which is "movable" in the sense that its location depends on the initial conditions of the differential equation.
Suppose we have an ordinary differential equation
in the complex domain. Any given solution y(x) of this equation may well have singularities at various points (i.e. points at which it is not a regular holomorphic function
, such as branch points, essential singularities
or poles). A singular point is said to be movable if its location depends on the particular solution we have chosen, rather than being fixed by the equation itself.
For example the equation
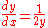
has solution
for any constant c. This solution has a branchpoint at 
, and so the equation has a movable branchpoint (since it depends on the choice of the solution, i.e. the choice of the constant c).
It is a basic feature of linear ordinary differential equations that singularities of solutions occur only at singularities of the equation, and so linear equations do not have movable singularities.
When attempting to look for 'good' nonlinear differential equations it is this property of linear equations that one would like to see: asking for no movable singularities is often too stringent, instead one often asks for the so-called Painlevé property
: 'any movable singularity should be a pole', first used by Sofia Kovalevskaya
.
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, a movable singularity is a point where the solution of the equation behaves badly
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
and which is "movable" in the sense that its location depends on the initial conditions of the differential equation.
Suppose we have an ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
in the complex domain. Any given solution y(x) of this equation may well have singularities at various points (i.e. points at which it is not a regular holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
, such as branch points, essential singularities
Essential singularity
In complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
or poles). A singular point is said to be movable if its location depends on the particular solution we have chosen, rather than being fixed by the equation itself.
For example the equation
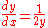
has solution
for any constant c. This solution has a branchpoint at , and so the equation has a movable branchpoint (since it depends on the choice of the solution, i.e. the choice of the constant c).It is a basic feature of linear ordinary differential equations that singularities of solutions occur only at singularities of the equation, and so linear equations do not have movable singularities.
When attempting to look for 'good' nonlinear differential equations it is this property of linear equations that one would like to see: asking for no movable singularities is often too stringent, instead one often asks for the so-called Painlevé property
Painlevé transcendents
In mathematics, Painlevé transcendents are solutions to certain nonlinear second-order ordinary differential equations in the complex plane with the Painlevé property , but which are not generally solvable in terms of elementary functions...
: 'any movable singularity should be a pole', first used by Sofia Kovalevskaya
Sofia Kovalevskaya
Sofia Vasilyevna Kovalevskaya , was the first major Russian female mathematician, responsible for important original contributions to analysis, differential equations and mechanics, and the first woman appointed to a full professorship in Northern Europe.She was also one of the first females to...
.