
Multi-scale approaches
Encyclopedia
The scale-space representation of a signal obtained by Gaussian
smoothing satisfies a number of special properties, scale-space axioms
, which make it into a special form of multi-scale representation. There are, however, also other types of 'multi-scale approaches' in the areas of computer vision
, image processing
and signal processing
, in particular the notion of wavelets. The purpose of this article is to describe a few of these approaches:
operation . For continuous signals, it holds that all scale-space kernels can be decomposed into the following sets of primitive smoothing kernels:
For discrete signals, we can, up to trivial translations and rescalings, decompose any discrete scale-space kernel into the following primitive operations:
the discrete Gaussian kernel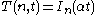 where
where 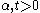 where
where 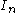 are the modified Bessel functions of integer order,
are the modified Bessel functions of integer order,
generalized binomial kernels corresponding to linear smoothing of the form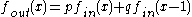 where
where 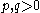
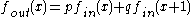 where
where 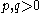 ,
,
first-order recursive filters corresponding to linear smoothing of the form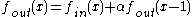 where
where 
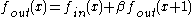 where
where  ,
,
the one-sided Poisson kernel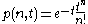 for
for 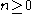 where
where 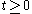
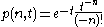 for
for 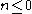 where
where 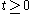 .
.
From this classification, it is apparent that it we require a continuous semi-group structure, there are only three classes of scale-space kernels with a continuous scale parameter; the Gaussian kernel which forms the scale-space of continuous signals, the discrete Gaussian kernel which forms the scale-space of discrete signals and the time-causal Poisson kernel that forms a temporal scale-space over discrete time. If we on the other hand sacrifice the continuous semi-group structure, there are more options:
For discrete signals, the use of generalized binomial kernels provides a formal basis for defining the smoothing operation in a pyramid. For temporal data, the one-sided truncated exponential kernels and the first-order recursive filters provide a way to define time-causal scale-spaces that allow for efficient numerical implementation and respect causality over time without access to the future. The first-order recursive filters also provide a framework for defining recursive approximations to the Gaussian kernel that in a weaker sense preserve some of the scale-space properties .
GAUSSIAN
Gaussian is a computational chemistry software program initially released in 1970 by John Pople and his research group at Carnegie-Mellon University as Gaussian 70. It has been continuously updated since then...
smoothing satisfies a number of special properties, scale-space axioms
Scale-space axioms
In image processing and computer vision, a scale-space framework can be used to represent an image as a family of gradually smoothed images. This framework is very general and a variety of scale-space representations exist...
, which make it into a special form of multi-scale representation. There are, however, also other types of 'multi-scale approaches' in the areas of computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, in particular the notion of wavelets. The purpose of this article is to describe a few of these approaches:
Scale-space theory for one-dimensional signals
For one-dimensional signals, there exists quite a well-developed theory for continuous and discrete kernels that guarantee that new local extrema or zero-crossings cannot be created by a convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
operation . For continuous signals, it holds that all scale-space kernels can be decomposed into the following sets of primitive smoothing kernels:
the Gaussian kernel
: where
where  ,
,
truncated exponential kernels (filters with one real pole in the s-plane):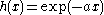 if
if 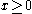 and 0 otherwise where
and 0 otherwise where 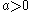
 if
if 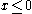 and 0 otherwise where
and 0 otherwise where 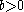 ,
,
translations,
rescalings.
For discrete signals, we can, up to trivial translations and rescalings, decompose any discrete scale-space kernel into the following primitive operations:
the discrete Gaussian kernel
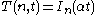 where
where 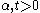 where
where 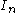 are the modified Bessel functions of integer order,
are the modified Bessel functions of integer order,generalized binomial kernels corresponding to linear smoothing of the form
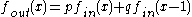 where
where 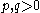
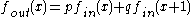 where
where 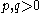 ,
,first-order recursive filters corresponding to linear smoothing of the form
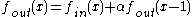 where
where 
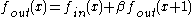 where
where  ,
,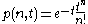 for
for 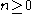 where
where 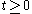
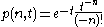 for
for 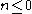 where
where 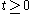 .
.From this classification, it is apparent that it we require a continuous semi-group structure, there are only three classes of scale-space kernels with a continuous scale parameter; the Gaussian kernel which forms the scale-space of continuous signals, the discrete Gaussian kernel which forms the scale-space of discrete signals and the time-causal Poisson kernel that forms a temporal scale-space over discrete time. If we on the other hand sacrifice the continuous semi-group structure, there are more options:
For discrete signals, the use of generalized binomial kernels provides a formal basis for defining the smoothing operation in a pyramid. For temporal data, the one-sided truncated exponential kernels and the first-order recursive filters provide a way to define time-causal scale-spaces that allow for efficient numerical implementation and respect causality over time without access to the future. The first-order recursive filters also provide a framework for defining recursive approximations to the Gaussian kernel that in a weaker sense preserve some of the scale-space properties .

